Коэффициенты взаимозависимости для номинального уровня измерения. 3 страница
Если извлеченную карточку не возвращать назад, а откладывать в сторону, то тот же процесс приведет нас к простой случайно бес повторной выборке размером в п единиц наблюдения или, как еще говорят, объемом в п единиц.
Описанная процедура простого случайного отбора становится чрезвычайно трудоемкой, если число N, задающее объем основы выборки, велико. Главная трудность состоит в том, что обеспечение равной вероятности попадания единицы наблюдения в выборочную совокупность требует очень тщательного перемешивания.
Чтобы устранить трудности, возникающие при исследовании больших генеральных совокупностей (а именно таких большинство в социологии), для реализации простого случайного отбора пользуются так называемыми таблицами случайных чисел. Они содержат те или иные случайные цифры, полученные путем реализации некоторого физического случайного процесса. В литературе приводятся различные последовательности случайных чисел объемом от нескольких десятков до миллиона цифр (табл. 14).
Продемонстрируем, как работать с таблицей случайных чисел, на гипотетическом примере, когда из совокупности заранее пронумерованных 300 единиц необходимо выбрить 7 единиц наблюдения. Поскольку N =300—трехзначное число, а в табл. 14 даны пятизначные числа, будем использовать только три последних цифры каждого числа. Таблица 14. Таблица случайных чисел
| Строка | (1) | (2) | (3) | (4) | (5) |
Начиная с первого числа, двигаясь по строке, получим первый номер 97. Числа более 300 пропускаем и, продолжая этот процесс далее, получим ряд чисел:
296, 209, 13, 157, 147, 32.
Это и есть номера единиц наблюдения, попавших в формируемую выборку.
При организации бесповторного отбора приходится пропускать и числа (если они попадаются), которые встречаются второй раз в этом ряду.
Начинать процесс выбора случайных чисел можно с любого места таблицы и вести его в любом направлении (по строкам, столбцам и т. п.) или выбирая только определенные столбцы. Если имеющиеся под рукой таблицы достаточно длинны, то при решении/ очередной задачи выбора рекомендуется начинать с нового места таблицы.
Расчет характеристик простой случайной выборки. Цель любого выборочного исследования состоит в том, чтобы, сформировав выборку, собрать по ней информацию и на основе этой информации оценить искомые характеристики генеральной совокупности.
Наиболее распространенной в социологических исследованиях задачей является оценка среднего значения признака (или доли в случае качественного признака) в генеральной совокупности.
Проиллюстрируем на примере нахождение выборочной оценки среднего генеральной совокупности. Предположим, что оценивается:
среднее число газет и общественно-политических журналов, выписываемых сотрудниками некоторого производственного коллектива, Рассмотрим по порядку все необходимые операции иих результаты.
Составляется основа выборки, т.е. список всех единиц отбора. В качестве такой основы может быть взят алфавитный список всех сотрудников, пронумерованных последовательно (табл. 15). В целях наглядности вместе с основой выборки приводятся и все истинные значения единиц отбора, еще неизвестные исследователю. В дальнейшем сопоставим истинное значение искомого параметра и выборочную оценку.
Таблица 15. Распределение членов коллектива по числу выписываемых газет и журналов
| Номер индивида (i) | Число выписываемых газет и журналов ( 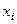 ) )
| Номер индивида (i) | Число выписываемых газет и журналов ( 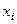 ) )
| Номер индивида (i) | Число выписываемых газет и журналов ( 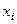 ) )
| Номер индивида (i) | Число выписываемых газет и журналов ( 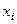 ) )
|
| N = 50 | 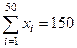
|
Общая сумма выписываемых газет п журналов равна 150. Среднее число выписываемых газет и журналов на каждого сотрудника равно ( m = 150/50 = 3.
Среднее квадратическое отклонение для генеральной совокупности равно
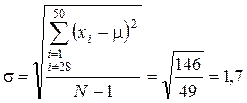
Сумма квадратов отклонений равна 146 при условии, что одно значение квадрата отклонения, а именно от единицы отбора 28, было исключено из суммы. Это значение, равное 49, резко увеличивает сумму, будучи нетипичным для генеральной совокупности. Такое исключение экстремального отклонения нередко применяется при обработке первичной социальной информации в том случае, когда предусмотрено возведение в квадрат, а само отклонение в 2 — 3 раза превышает среднее значение параметра.
Однако ни среднее значение параметра, ни среднее квадратическое отклонение перед началом исследования не известны. В противном случае само исследование было бы излишним.
Естественно предположить при анализе вышеприведенного примера, что каждый респондент (единица отбора и единица наблюдения) выписывает несколько газет и журналов и что количество выписываемых газет и журналов не слишком сильно варьирует (если бы путем выборочного исследования потребовалось определить, скажем, объем личных библиотек, положение исследователя осложнилось бы). Исходя из этих соображений, полагаем достаточной выборку, состоящую из пяти респондентов. Проверить правильность определения объема выборки можно только после обработки результатов пилотажного исследования.
Предположим, что случайный выбор из табл. 15 дал следующие результаты: выбраны номера 18, 4, 28, 39, 22; они соответствуют значениям признаков 4, 0, 10, 4, 4.
Среднее арифметическое по выборке х = 22/5 = 4,4, дисперсия
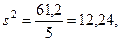 а
а 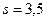
Такое значительное отклонение от истинного значения средней объясняется тем, что в выборку попал респондент № 28, исключенный при подсчете дисперсии для генеральной совокупности как нетипичный. Однако при формировании выборки еще неизвестно, что данный респондент нетипичен. Но сам факт, что среднее квадратическое отклонение приближается по величине к средней, должен насторожить исследователей.
Для большей наглядности выразим s в процентах от величины средней: (3,5 : 4,4) 100% = 79%, т. е. среднее отклонение значений признака от выборочной средней арифметической величины составляет 79 %. В таких случаях целесообразно увеличить объем выборки, например, в 2 раза. В результате были отобраны номера: 44, 2, 12, 26, 14, 27, 35, 9, 8, 49; значения признака 5, 2, 4, 6, 1, 3, 2, 5, 3. 4.
Среднее арифметическое — 3,6, дисперсия 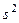 = 2,26, среднее квадратическое отклонение = 1,5. Теперь оно составляет приблизительно 40% от величины средней. При больших дисперсиях объем выборки увеличивают с учетом практических возможностей до тех пор, пока дисперсия не перестает уменьшаться. Дальнейшее увеличение объема выборки является нецелесообразным. Обычно исследователь приходит к некоторому компромиссному решению относительно объема выборки в зависимости от требуемой точности, а также средств и времени, которыми он располагает.
= 2,26, среднее квадратическое отклонение = 1,5. Теперь оно составляет приблизительно 40% от величины средней. При больших дисперсиях объем выборки увеличивают с учетом практических возможностей до тех пор, пока дисперсия не перестает уменьшаться. Дальнейшее увеличение объема выборки является нецелесообразным. Обычно исследователь приходит к некоторому компромиссному решению относительно объема выборки в зависимости от требуемой точности, а также средств и времени, которыми он располагает.
Сводка необходимых формул для простой случайной выборки. В рассмотренном гипотетическом примере легко было оценить качество выборочной оценки среднего (перед глазами была информация обо всей генеральной совокупности). Но как провести его оценку
в реальном исследовании, когда имеется только информация, полученная из выборки?
На помощь приходит статистическая теория выборочного метода Она позволяет при условии реализации случайного отбора достичь по крайней мере следующих двух целей:
1. По заданной априори необходимой степени точности выводов (формализуемой с помощью понятия доверительной вероятности) найти, возможные интервалы, изменения характеристик генеральной совокупности (доверительные интервалы). И наоборот, рассчитать доверительную вероятность отклонения характеристики генеральной совокупности от выборочной по заданной величине доверительного интервала.
2. Найти объем планируемой выборки, позволяющей достигнуть в пределах требуемой точности расчета выборочных характеристик необходимую доверительную вероятность.
Дадим сводку необходимых для достижения этих целей формул[117].
Чтобы уметь применять приведенные формулы при планировании выборки в эмпирическом социологическом исследовании, познакомимся несколько подробнее с основными понятиями выборочного метода — доверительная вероятность и доверительный интервал.
Теоретико-вероятностные теоремы, восходящие к закону больших чисел, позволяют с Определенной вероятностью, обозначаемой (1-a), утверждать, что для изучаемого признака отклонения выборочной средней от генеральной не превысят некоторой величины А, называемой предельной ошибкой выборки.
В одной из формулировок это утверждение записывается следующим образом:
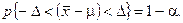 (1)
(1)
Используя формулу табл. 16 для предельной ошибки 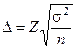 , при повторном случайном отборе получим выражение
, при повторном случайном отборе получим выражение
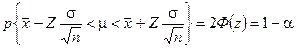
где 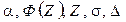 описаны в примечании к табл. 16. Смысл приведенного соотношения следующий: с доверительной вероятностью (1-a) можно утверждать, что генеральное среднее лежит в интервале
описаны в примечании к табл. 16. Смысл приведенного соотношения следующий: с доверительной вероятностью (1-a) можно утверждать, что генеральное среднее лежит в интервале 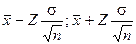 , который и называется доверительным интервалом, к определяет как бы степень доверия к данным, получаемым по рассчитанным с его помощью выборочным характеристикам. Отсюда и название a — уровень значимости.
, который и называется доверительным интервалом, к определяет как бы степень доверия к данным, получаемым по рассчитанным с его помощью выборочным характеристикам. Отсюда и название a — уровень значимости.
Таблица 16.Сводная таблица формул для расчета характеристик простой случайной выборки
| Способ отбора | Отбор по качественному признаку (для доли) | ||
| средняя ошибка | предельная ошибка | объем выборки | |
| Повторный случайный | 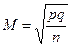
| 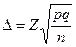
| 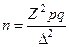
|
| Бесповторный случайный | 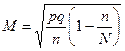
| 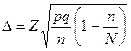
| 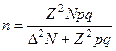
|
| Способ отбора | Отбор по количественному признаку (для средней) | ||
| средняя ошибка | предельная ошибка | объем выборки | |
| Повторный случайный | 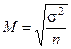
| 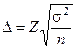
| 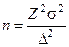
|
| Бесповторный случайный | 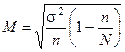
| 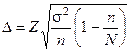
| 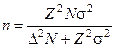
|
Обозначения: М — средняя ошибка выборки, р — доля единиц с данным значением признака, q = 1 — р — доля единиц, в которых этот признак отсутствует, n — объем выборки, N — объем генеральной совокупности, 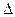 — предельная ошибка, Z — числа, определяемые по таблице критических точек стандартного нормального распределения (см. табл. А приложения), a — уровень значимости,
— предельная ошибка, Z — числа, определяемые по таблице критических точек стандартного нормального распределения (см. табл. А приложения), a — уровень значимости, 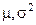 — генеральные среднее и дисперсия.
— генеральные среднее и дисперсия.
Примечание. При расчете характеристик бесповторного случайного отбора, с которым практически всегда имеет дело социолог, можно пользоваться более простыми формулами для случая повторного отбора, если объем генеральной совокупности значительно больше объема выборки.
Принятие того или иного уровня значимости, например 5%-ного (a = 0,05), зависит от целей данного социологического исследования, требований к степени гарантии его результатов. Социолог должен четко понимать,, что, выбрав, скажем, уровень значимости, равный 5%, и рассчитав на основе его выборочные характеристики, мы будем утверждать наличие некоторого эффекта, который на самом деле может оказаться несправедливым приблизительно в пяти процентах случаев.
Пример. При обследовании 900 человек — лиц трудоспособного возраста — определен их средний возраст. Для вероятности 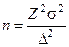 = 0,90 необходимо найти доверительный интервал, в котором содержится генеральное среднее. Поскольку дисперсия признака неизвестна, оцепим ее приблизительно по значению размаха для генеральной совокупности.
= 0,90 необходимо найти доверительный интервал, в котором содержится генеральное среднее. Поскольку дисперсия признака неизвестна, оцепим ее приблизительно по значению размаха для генеральной совокупности.
С этой целью воспользуемся соотношением связи среднего квадратичного отклонения о размахом
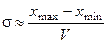 , (3)
, (3)
справедливым в предположении нормального характера распределения. Здесь 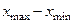 — вариационный размах генеральной совокупности, а V — величина, зависящая от объема выборки, значения которой можно найти в табл. 17.
— вариационный размах генеральной совокупности, а V — величина, зависящая от объема выборки, значения которой можно найти в табл. 17.
Так как по всей генеральной совокупности верхняя граница трудоспособности в СССР — 60 лет, а нижняя — 16, то 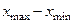 = 60 – 16 = 44, следовательно (для п³100 —последний столбец
= 60 – 16 = 44, следовательно (для п³100 —последний столбец
Таблица 17
| Объем выборки n | ||||||
| V | 2,3 | 3,1 | 3,7 | 4,1 | 4,5 | 5,0 |
табл. 17), получим приближенное значение среднеквадратичного отклонения 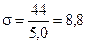 .
.
Пользуясь выражением для средней ошибки простого случайного повторного отбора (см. табл. 16) 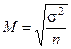 , получим
, получим 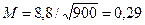 . Предельная ошибка рассчитывается по формуле
. Предельная ошибка рассчитывается по формуле 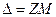 (см. табл. 16).
(см. табл. 16).
ВеличинаZ, находится по табл. А приложения при a/2. Таким образом, если (1-a) = 0,9, то Z = 1,64.
Подставляя найденные значения М и Z в формулу предельной ошибки, получаем 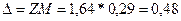 .
.
Таким образом, округляя значение ошибки до половины года (0,5), можно утверждать, что с вероятностью 0,9 генеральное среднее не выйдет за пределы интервала 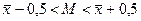 , т. е. точность выборочной оценки среднего, рассчитанной по нашей выборке (если она организована методом простого случайного повторного отбора), оказывается равной половине года. Утверждать это мы можем с вероятностью 0,9. Интервал
, т. е. точность выборочной оценки среднего, рассчитанной по нашей выборке (если она организована методом простого случайного повторного отбора), оказывается равной половине года. Утверждать это мы можем с вероятностью 0,9. Интервал 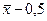 ,
, 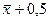 и задает доверительный интервал, рассчитанный по доверительной вероятности, равной 0,9.
и задает доверительный интервал, рассчитанный по доверительной вероятности, равной 0,9.
Теперь рассмотрим методику нахождения доверительного интервала по заданной доверительной вероятности для качественного признака.
Пример. Выборочное обследование 900 человек, организованное по способу простого случайного повторного отбора, показало, что 18 человек не информированы о крупном событии в стране. Для доверительной вероятности 0,95 нужно найти доверительный интервал.
Пользуясь выражением для формулы средней ошибки (см. табл. 16) 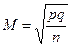 , получаем
, получаем 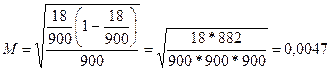 .
.
Далее по табл. А приложения, как уже описывалось выше, для a/2 находим Z = 1,96.
Теперь можно определить величину предельной ошибки (см. табл. 16):
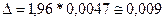 или 0,9%
или 0,9%
Таким образом, доверительные границы для доли неинформированных в генеральной совокупности равны 0,02 ± 0,009, или от 1,1 до 2,9%.
Приведем иллюстративный пример определения объема простой повторной случайной выборки. Как видно из формул, чтобы определить объем (см. табл. 16), дл его оценки необходимо знать дисперсии генеральной средней или хотя бы ее оценки.
Для применения соответствующей формулы необходимо оцепить значение дисперсии, что можно сделать (при отсутствии информации о ней и о размахе значений признака в генеральной совокупности) путем проведения одной - двух пилотажных (пробных) выборок.
Допустим, что в результате пилотажа выборочная оценка дисперсии равна 12,24. Определим, каким должен быть объем выборки, чтобы с вероятностью 0,95 предельное отклонение выборочной средней от генеральной не превышало одного экземпляра газет. При этих условиях получаем численность планируемой выборки
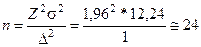 .
.
Таким образом, объем выборки должен составлять 24 человека.
3. Систематическая и серийная выборки
Систематический отбор. В Социологических исследованиях иногда применяется несколько упрощенный вариант простого случайного отбора, который носит название систематического. Основа выборки для него характеризуется теми же требованиями, что и для Простого случайного отбора. Иными словами, основу выборки составляют различные алфавитные списки, картотеки учреждений, домовые книги и т. п. При систематическом отборе выбор единиц наблюдения осуществляется через один и тот же интервал k из исходного списка. Например, при k = 20 выбирается 3, 23, 43, 63 и т. д. единиц списка.
Таким образом, элементы выборочной совокупности однозначно определяются при систематическом отборе номером первого элемента (тройки в нашем примере) и величиной интервала .
В одной из схем систематического отбора в качестве первого элемента выбирается средний элемент списка или стоящий рядом с ним. Так, если список генеральной совокупности пронумерован от 1 до N, то номер первого элемента может быть определен по формулам 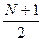 , если N — нечетное и N/2, если N — четное число.
, если N — нечетное и N/2, если N — четное число.
Более распространен выбор первой единицы отбора случайным образом (например, по таблице случайных чисел).
Величина А зависит от характера поставленной проблемы, от разброса значений исследуемой характеристики генеральной совокупности.
Если решен вопрос об объеме планируемой выборки, то число определяется в зависимости от объема генеральной совокупности и объема выборки (n).
Если N — кратное числа n, то интервал определяется по формуле 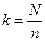 . Если N некратно n, то реальный объем выборки
. Если N некратно n, то реальный объем выборки 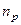 и планируемый объем
и планируемый объем 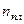 при различных способах вычисления числа k связаны следующими соотношениями:
при различных способах вычисления числа k связаны следующими соотношениями:
если 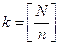 , то
, то 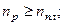
если 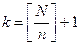 , то
, то 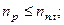
Здесь [ ] означает целую часть числа.
Поясним сказанное на примере: пусть N = 19 и n = 5, чему равно k? Тогда k равно либо 3, либо 4.
При k = 3 в выборку попадает больше пяти элементов в данном случае 6 или 7. При k = 4 в выборку попадут пять или четыре элемента.
Расчет характеристик систематической выборки. В связи с тем что систематическая выборка определяется как разновидность простого случайного отбора, ее характеристики рассчитываются с помощью соответствующих формул табл. 16.
В примере с подписчиками газет и журналов (см. табл. ,15) в систематическую выборку объемом 5 единиц попали номера респондентов 10, 20, 30, 40, 50, для которых соответствующее число выписываемых газет равно 3, 5, 5, 3, 2. Среднее по выборке равно 3,6, а дисперсия — 1,44 ( = 1,2).
Применяя для простоты формулы повторной случайной выборки, получаем 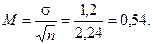
Таким образом, с вероятностью 0,95 можно утверждать, что доверительный интервал для генеральной средней имеет следующие границы: (3,6 ± 1,96 0,54) = (3,6 ± 1,05) = (2,55; 4,65).
Возможности и ограничения систематической выборки. Систематическая выборка является экономными удобным способом формирования выборочной совокупности. Однако при ее применении в социологических исследованиях необходимо следить за тем, чтобы; список, используемый в качестве основы выборки, не обладал порядком, отражающим периодичность в значениях изучаемой характеристики.
Проиллюстрируем это положение. При составлении основы выборки для опроса рабочих в одном из цехов завода выбранный интервал может совпасть с числом рабочих в бригаде, в списке которой первым окажется бригадир. При систематическом отборе повышаются шансы попадания в выборку только одних бригадиров. При такой реализации выборки повышается вероятность получения значительных систематических ошибок.
Предварительное расположение элементов генеральной совокупности по убыванию или возрастанию исследуемой характеристики позволит избавиться от этой опасности. Так, если в рассмотренном примере основа выборки организуется на базе платежной ведомости, в которой лица расположены в порядке возрастания их заработной платы, то опасность попадания только на одних бригадиров исключается.
Систематическая выборка из-за простоты реализации получила широкое применение в социологических исследованиях.
Серийная (гнездовая) выборка. При серийной выборке единицы отбора представляют собой статистические серии, т. е. совокупности статистически различимых единиц. В качестве таких единиц могут выступать семья, бригада, школьный класс, небольшие производственные коллективы в учреждениях, почтовые отделения, врачебные участки, населенные пункты, территориальные общности и т. п. Отобранные в выборку серии подвергаются сплошному или выборочному обследованию. Второй вариант используется в практике социологических исследований гораздо чаще, чем первый. Собственно говоря, любая многоступенчатая выборка представляет собой гнездовую выборку, в которой единицы отбора на высших ступенях являются гнездами из единиц отбора нижних ступеней.
Организация серийной выборки. Серийная выборка имеет существенные организационные преимущества перед простой случайной выборкой, так как значительно легче произвести отбор и изучение нескольких коллективов, бригад, цехов и т. д., находящихся на одном месте, чем нескольких сотен пространственно разбросанных людей. Процедура отбора позволяет сконцентрировать выборку в сравнительно небольшом числе пунктов.
Серийная выборка может организовываться по схемам простой случайной и систематической выборок. Наконец, она может формироваться после предварительного районирования генеральной совокупности.
В первых двух случаях к информации о генеральной совокупности — основе выборки — предъявляются те же требования, что и ко всем вероятностным выборкам: размещение элементов генеральной совокупности (серий) не должно быть каким-либо образом систематизировано.
Метод маршрутного опроса. Этот метод социологи часто используют, когда единицей наблюдения выступает семья.
В выборочную совокупность, например, намечено включить определенное число случайно отобранных семей или квартир. На карте города или населенного пункта нумеруются все улицы. С помощью таблицы случайных чисел отбираются большие числа, которые позволяют идентифицировать семьи или квартиры, попавшие в выборку. Каждое большое число рассматривается как состоящее из трех компонентов: первые две или три цифры в нем указывают номер улицы, следующая цифра — номер дома, последняя цифра — номер квартиры в выбранном доме.
Например, число 42—25—3 указывает квартиру № 3 дома № 25 на 42-й улице.
Организация серийной выборки методом маршрутного опроса наиболее приспособлена к городам, где преобладают отдельные квартиры, или к населенным пунктам, где еще сохраняется частное домовладение (в последнем случае отпадает необходимость выбирать номер квартиры).
Возможности и ограничения серийной выборки. При серийной выборке всегда имеет место занижение по сравнению с генеральной совокупностью дисперсии изучаемого признака в силу определенного сходства единиц в сериях.
Например, вполне объяснима заметная связь между членами семьи. Характер профессий детей в определенной мере может зависеть от профессии родителей. Очевидна связь членов семьи в отношении их социальной принадлежности.
С точки зрения статистика, сходство элементов серий приводит к избыточности однотипной, повторяющейся информации. Социолог должен учитывать этот органически присущий серийной выборке статистический порок при прочих равных условиях, выбирая в качестве гнезд такие общности, которые содержат максимально разнородные конечные единицы наблюдения. Так, при изучении, скажем, качества медицинского обслуживания населения города разумно в виде гнезд выбрать совокупность жителей, обслуживаемых отдельными почтовыми отделениями, или проживающих на территории отдельных ЖЭКов, но никак не врачебные участки, поскольку последний выбор привел бы к искажению результатов.
Расчет характеристик серийной выборки. Расчет характеристик серийной выборки имеет некоторое отличие от простой случайной и систематической выборок. Это отличие связано прежде всего с вычислением дисперсий и ошибки выборки.
Вычисление средней ошибки серийной выборки основано на дисперсии серийных средних.
Пример. Из генеральной совокупности, включающей 16 семей, сделана серийная выборка, состоящая из четырех семей (в каждой семье по 4 человека)[118]. Перед исследователями стоит задача найти оценку средней заработной платы в генеральной совокупности, оценку ее дисперсии и среднюю ошибку выборки (табл. 18).
Средняя ошибка бесповторной серийной выборки определяется по формуле
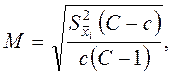
где 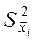 — дисперсия серийных средних; С — число серий в генеральной совокупности (равных по численности); с — число серий в выборке.
— дисперсия серийных средних; С — число серий в генеральной совокупности (равных по численности); с — число серий в выборке.
Таблица 18.Данные для примера
| Семья | Заработная плата работающих членов семьи (x), руб. | Средняя заработная плата семьи 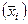 , руб. , руб.
| |||
| 81,75 86,75 86,75 78,75 | |||||
Расчет дисперсии серийных средних:
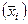
| 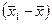
| 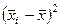
|
| 81,75 86,75 86,75 78,75 | —1,75 3,25 3,25 —4,75 | 3,0625 10,5625 10,5625 22,5625 |
| x = 83,5 | å = 46,75 |
Дата добавления: 2015-09-29; просмотров: 958;
