СХЕМА 3 6 страница
 (32)
(32)
Так, для вышеприведенного примера он равен

Множественный коэффициент корреляции показывает, что включение признаков 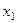 и
и 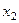 в уравнение
в уравнение

на 32% объясняет изменчивость результатирующего фактора. Чем больше  , тем полнее независимые переменные
, тем полнее независимые переменные  описывают признак у. Обычно R служит критерием включения или исключения новой переменной в регрессионное уравнение. Если R мало изменяется при включении новой переменной в уравнение, то такая переменная отбрасывается.
описывают признак у. Обычно R служит критерием включения или исключения новой переменной в регрессионное уравнение. Если R мало изменяется при включении новой переменной в уравнение, то такая переменная отбрасывается.
Корреляционное отношение. Наиболее общим показателем связи при любой форме зависимости между переменными является корреляционное отношение 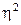 . Корреляционное отношение
. Корреляционное отношение 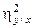 определяется через отношение межгрупповой дисперсии к общей дисперсии по признаку y:
определяется через отношение межгрупповой дисперсии к общей дисперсии по признаку y:
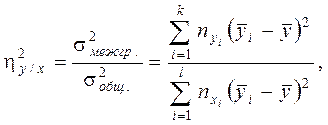 (33)
(33)
где  — среднее значение i-го у-сечения (среднее признака у для объектов, у которых
— среднее значение i-го у-сечения (среднее признака у для объектов, у которых  =
= 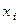 т. е. столбец «i»);
т. е. столбец «i»); 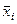 — среднее значение i-го x-сечения (т. е. строка «i»);
— среднее значение i-го x-сечения (т. е. строка «i»);  —число наблюдений в у-сечении;
—число наблюдений в у-сечении;  — число наблюдений в x-сечении;
— число наблюдений в x-сечении;  — среднее значение у.
— среднее значение у.
Величина 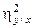 показывает, какая доля изменчивости значений у обусловлена изменением значения х. В отличие от коэффициента корреляции
показывает, какая доля изменчивости значений у обусловлена изменением значения х. В отличие от коэффициента корреляции 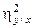 не является симметричным показателем связи, т. е.
не является симметричным показателем связи, т. е. 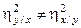 . Аналогично определяется корреляционное отношение х по у[95].
. Аналогично определяется корреляционное отношение х по у[95].
Пример. По данным таблицы сопряженности (табл. 9) найдем 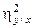 .
.
Вычислим общую среднюю

Тогда

Сравнение статистических показателей r и  . Приведем сравнительную характеристику коэффициента корреляции (будем сравнивать r2) и корреляционного отношения
. Приведем сравнительную характеристику коэффициента корреляции (будем сравнивать r2) и корреляционного отношения  :
:
а) r2 = 0, если х и у независимы (обратное утверждение неверно);
б) r2 = 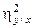 = 1 тогда и только тогда, когда имеется строгая линейная функциональная зависимость у от х;
= 1 тогда и только тогда, когда имеется строгая линейная функциональная зависимость у от х;
в) r2 = 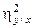 <1 тогда и только тогда, когда регрессия х и у строго линейна, но нет функциональной зависимости;
<1 тогда и только тогда, когда регрессия х и у строго линейна, но нет функциональной зависимости;
г) r2< 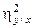 <1 указывает на то, что нет функциональной зависимости и существует нелинейная кривая регрессии.
<1 указывает на то, что нет функциональной зависимости и существует нелинейная кривая регрессии.
Таблица 9.Вычисление 
Середина интервала 
| Середина интервала 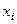
| 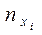
| ||
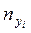

|
Коэффициенты взаимозависимости для порядкового уровня измерения. К этой группе относятся коэффициенты ранговой корреляции Спирмена 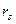 , Кендалла
, Кендалла 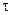 и
и 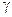 . Коэффициенты ранговой корреляции используются для измерения взаимозависимости между качественными признаками, значения которых могут быть упорядочены или проранжированы по степени убывания (или нарастания) данного качества у исследуемых социальных объектов.
. Коэффициенты ранговой корреляции используются для измерения взаимозависимости между качественными признаками, значения которых могут быть упорядочены или проранжированы по степени убывания (или нарастания) данного качества у исследуемых социальных объектов.
Коэффициент ранговой корреляции Спирмена 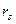 . Этот коэффициент вычисляется по следующей формуле:
. Этот коэффициент вычисляется по следующей формуле:

где 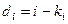 — разность между i-ми парами рангов; l — число сопоставляемых пар рангов. Величина
— разность между i-ми парами рангов; l — число сопоставляемых пар рангов. Величина 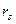 может изменяться в пределах от +1 до—1, когда два ряда проранжированы в одном порядке. При полном взаимном беспорядочном расположении рангов
может изменяться в пределах от +1 до—1, когда два ряда проранжированы в одном порядке. При полном взаимном беспорядочном расположении рангов 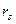 равен нулю.
равен нулю.
Пример. По данным табл. 10 выясним, в какой степени связаны жизненные планы детей, отличающихся по социальному происхождению. Для этого проранжируем значения процентных распределении для каждой из двух групп детей.
В графе «из крестьян» (табл. 10) встречаются два одинаковых числа (51, 0). В подобных случаях обоим числам присваивают ранг, равный среднему арифметическому из этих рангов, т. е. (3 + 4)/2 = 3,5. Подставляя промежуточные величины, вычисленные в табл. 10, в формулу (34), находим[96]

Такую величину 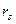 можно интерпретировать как высокую степень связи между жизненными планами детей рабочих и крестьян. Однако большая величина
можно интерпретировать как высокую степень связи между жизненными планами детей рабочих и крестьян. Однако большая величина 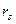 не должна скрывать тот факт, что жизненные планы молодежи в табл. 10 распадаются на две группы. Для одной группы (нижняя часть таблицы) ранги полностью совпадают, а для другой (верхняя часть) — нет.
не должна скрывать тот факт, что жизненные планы молодежи в табл. 10 распадаются на две группы. Для одной группы (нижняя часть таблицы) ранги полностью совпадают, а для другой (верхняя часть) — нет.
Таблица 10*
| Жизненные планы | Социальное происхождение | Ранг I | Ранг II | 
| 
| |
| из рабочих | из крестьян | |||||
| Получить высшее образование Получить интересную любимую работу Побывать в других странах Создать себе хорошие жилищные условия Добиться хорошего материального обеспечения Повысить свою квалификацию Получить среднее образование Поехать на одну из новостроек | 57,5 57,3 53,8 49,7 48,5 42,0 22,6 19,4 | 51,0 59,0 52,0 51,0 50,0 45,0 32,0 25,0 | 3,5 3,5 | -2,5 0,5 | 6,25 0,25 |
* Лиеовский В. Эскиз к портрету. М., 1969, с. 42. Распределение респондентов в таблице приведено в процентах к численности групп из рабочих, из крестьян соответственно. Поскольку респонденты могли выбирать при опросе более чем один жизненный план, то сумма по столбцам не равна 100%.
Если подсчитать 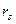 для каждой группы отдельно, то в первом случае, очевидно,
для каждой группы отдельно, то в первом случае, очевидно, 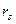 = 1, а во втором
= 1, а во втором 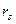 = 0,15, но статистически незначимо отличается от 0.
= 0,15, но статистически незначимо отличается от 0.
Значимость коэффициента корреляции Спирмена для l£100 можно определить по табл. Г приложения, где приведены критические величины 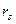 .
.
Если l>100, то критические значения находятся по табл. А приложения. Наблюдаемые значения критерия вычисляются по формуле
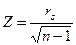 . (35)
. (35)
Например, возвращаясь к данным табл. 10, где l<100, по табл. Г приложения найдем, что для того, чтобы 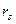 был значим на уровне 0,01, он должен быть равен или превосходить 0,833. Эмпирическое значение
был значим на уровне 0,01, он должен быть равен или превосходить 0,833. Эмпирическое значение 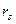 = 0,9, и поэтому делается вывод, что имеется значимая связь между предпочтениями жизненных планов двух групп респондентов. Аналогичным образом легко убедиться, что
= 0,9, и поэтому делается вывод, что имеется значимая связь между предпочтениями жизненных планов двух групп респондентов. Аналогичным образом легко убедиться, что 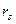 = 0,15 при l = 4 статистически незначим.
= 0,15 при l = 4 статистически незначим.
Коэффициент ранговой корреляции 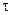 Кендалла. Подобно
Кендалла. Подобно 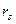 , коэффициент Кендалла используется для измерения взаимосвязи между качественными признаками, характеризующими объекты одной и той же природы, ранжированные по одному и тему же критерию
, коэффициент Кендалла используется для измерения взаимосвязи между качественными признаками, характеризующими объекты одной и той же природы, ранжированные по одному и тему же критерию 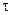 изменяется от +1 до —1.
изменяется от +1 до —1.
Для расчета  используется формула
используется формула
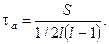 (36)
(36)
Как вычисляется S, поясним на примере данных табл. 10.
Таблица упорядочена так, что в графе «Ранг I» ранги расположились в порядке возрастания их значений. Берем значение ранга, стоящего в графе Ранг II на первом месте, 3,5; из расположенных ниже данного ранга семи других четыре значения его превышают, а два — меньше его. Число 4 записывается в графу  , а 2 в колонку
, а 2 в колонку 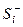 . Аналогичный подсчет делается для второго ранга со значением 1. Число рангов, расположенных ниже данного значения и превышающих его, равно 6, а число рангов, меньших данного,— 0 и т. д. Остальные вычисления ясны из следующей таблицы:
. Аналогичный подсчет делается для второго ранга со значением 1. Число рангов, расположенных ниже данного значения и превышающих его, равно 6, а число рангов, меньших данного,— 0 и т. д. Остальные вычисления ясны из следующей таблицы:

| 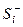
| 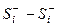
| 
| 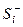
| 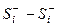
|

|
Тогда, подставив соответствующие значения в формулу (36), получим
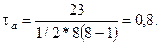
Таким образом,  дает более осторожную оценку для степени связи двух признаков, чем
дает более осторожную оценку для степени связи двух признаков, чем 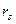 .
.
При расчете  не учитывались равные ранги. Например, в табл. 10 имеются два равных ранга со значением 3,5. Если число равных рангов велико, то необходимо вычислить
не учитывались равные ранги. Например, в табл. 10 имеются два равных ранга со значением 3,5. Если число равных рангов велико, то необходимо вычислить 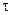 по следующей формуле:
по следующей формуле:
 (37)
(37)
где  (
( 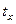 — число равных рангов по первой переменной);
— число равных рангов по первой переменной); 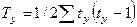 (
(  — число равных рангов по второй переменной). Для предыдущего примера
— число равных рангов по второй переменной). Для предыдущего примера 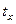 = 1,
= 1,  = 2, тогда
= 2, тогда 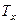 = 0,
= 0,  = 1.
= 1.
Значимость коэффициента корреляции Кендалла  при l>10 определяется по формуле
при l>10 определяется по формуле
 (38)
(38)
Гипотеза о том, что  = 0, будет отвергнута для данного a если
= 0, будет отвергнута для данного a если  .
.
Для вышеприведенного примера

По табл. А приложения для a = 0,05 находим  , равное 1,96. Поскольку расчетное значение Z = 2,84 и, следовательно, больше
, равное 1,96. Поскольку расчетное значение Z = 2,84 и, следовательно, больше 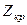 заключаем с вероятностью 95%, что
заключаем с вероятностью 95%, что 
Коэффициенты корреляции Спирмена и Кендалла используются как меры взаимозависимости между рядами рангов, а не как меры связи между самими переменными. Так, в табл. 10 ранги отражают иерархию жизненных планов, но совершенно не говорят о том, что дети рабочих почти в равной мере хотят получить как высшее образование, так и интересную работу (разница 0,2%), а дети крестьян в большей степени стремятся к высшему образованию (разница 8%). Кроме того, какая-нибудь из групп респондентов может считать, что выделенные категории вообще не отражают их жизненных планов, но проранжировали предложенные варианты. Если для целей исследования можно предположить эти моменты несущественными, то оправданно применение ранговой корреляции.
Коэффициенты Спирмена и Кендалла обладают примерно одинаковыми свойствами, но т в случае многих рангов, а также при введении дополнительных объектов в ходе исследования имеет определенные вычислительные преимущества[97].
Другая мера связи между двумя упорядоченными переменными — у. Она, так же как и предыдущие коэффициенты, изменяется от +1 до —1 и может быть подсчитана при любом числе связанных рангов. Формула для вычисления записывается в виде

Для иллюстрации правил вычисления 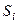 , по сгруппированным данным обратимся к примеру (табл. 11).
, по сгруппированным данным обратимся к примеру (табл. 11).
Таблица 11. Распределение ответивших на вопрос: «Устраивает ли Вас Ваша настоящая работа» — в зависимости от стажа работы в бригаде
| Альтернативы ответа | Стаж работы | Сумма | |||
| до 1 года | 1-2 года | 2-5 лет | 5 и более | ||
| Устраивает Не устраивает | |||||
| Сумма |
Процесс вычисления  и
и  наглядно представлен па схеме (схема 2).
наглядно представлен па схеме (схема 2).

| + | + | ||||||||||||

| + | + | ||||||||||||
СХЕМА 2. Схема вычисления  и
и 
Так:

Подставляя эти величины в формулу для 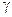 , находим
, находим
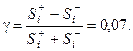
Проверку статистической значимости проводят по формуле

Гипотеза H0 о равенстве нулю коэффициента отвергается, если 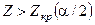 . Для наших данных
. Для наших данных

Для a = 0,05 по табл. А приложения 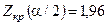 . Таким образом,
. Таким образом,  , и, следовательно, у нас нет оснований отвергнуть гипотезу Н0:
, и, следовательно, у нас нет оснований отвергнуть гипотезу Н0: 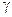 = 0, т. е. лишь в 5 % случаев следует ожидать, что
= 0, т. е. лишь в 5 % случаев следует ожидать, что 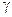 будет отличен от нуля.
будет отличен от нуля.
Множественный коэффициент корреляции W. Этот коэффициент, иногда называемый коэффициентом конкордации, используется для измерения степени согласованности двух или нескольких рядов проранжированных значений переменных.
Коэффициент W вычисляется по формуле

где k — число переменных; п — число индивидов или категорий, которые ранжируются; 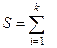 (сумма рангов по строке — а)2; а - среднее из суммы рангов.
(сумма рангов по строке — а)2; а - среднее из суммы рангов.
Таблица 12. Вычисление множественного коэффициента ранговой корреляции
| Респондент | Удовлетворенность по признакам А, Б, В | Сумма рангов | ||
| А | Б | В | ||
| 1-й 2-й 3-й 4-й 5-й | ||||
| n = 5 | 
|
Для данных табл. 12 а = 45/5 = 9;

Значимость полученной величины W для п>7 проверяется по критерию 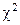 .
.
 (41)
(41)
со степенью свободы n—1. Для примера 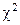 = 10,133, степень свободы (n—1) = 4. Для a = 0,05 из табл. Б приложения находим
= 10,133, степень свободы (n—1) = 4. Для a = 0,05 из табл. Б приложения находим 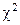 = 9,488. Поскольку наблюдаемое значение
= 9,488. Поскольку наблюдаемое значение 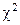 больше критической точки, отвергаем гипотезу о том, что не существует значимой связи между рассматриваемыми переменными[98].
больше критической точки, отвергаем гипотезу о том, что не существует значимой связи между рассматриваемыми переменными[98].
Дата добавления: 2015-09-29; просмотров: 788;
