Коэффициенты взаимозависимости для номинального уровня измерения. 2 страница
Первый подход предложен Г. С. Лбовым[111]. Автор предполагает, что исходные признаки могут быть измерены по любой шкале, и следующим образом вводит понятие логического, высказывания, являющегося основным во всех предложенных им алгоритмах.
Если признак 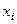 , измерен по номинальной шкале и
, измерен по номинальной шкале и 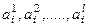 — его значения, то назовем элементарным высказыванием выражение вида
— его значения, то назовем элементарным высказыванием выражение вида 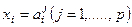 . Если признак
. Если признак 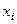 , измерен по шкале, тип которой не ниже порядковой шкалы, b и с — произвольные его возможные значения и b<с, то назовем элементарным высказыванием выражение вида b<
, измерен по шкале, тип которой не ниже порядковой шкалы, b и с — произвольные его возможные значения и b<с, то назовем элементарным высказыванием выражение вида b< 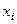 <c. Логическим высказыванием назовем выражение вида
<c. Логическим высказыванием назовем выражение вида 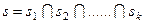 , где
, где 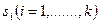 — произвольное элементарное высказывание, а
— произвольное элементарное высказывание, а 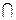 — знак конъюнкции (логический символ: высказывание, являющееся конъюнкцией двух предложений, истинно в том случае, если истинны оба входящие в него предложения).
— знак конъюнкции (логический символ: высказывание, являющееся конъюнкцией двух предложений, истинно в том случае, если истинны оба входящие в него предложения).
Приведем пример логической закономерности. Пусть 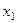 — пол, принимающий два значения: 0 (мужчина) и 1 (женщина);
— пол, принимающий два значения: 0 (мужчина) и 1 (женщина); 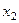 — удовлетворенность респондента своей работой, измеренная по порядковой шкале с градациями 1, ..., 5;
— удовлетворенность респондента своей работой, измеренная по порядковой шкале с градациями 1, ..., 5; 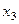 — зарплата респондента, измеренная по шкале отношений (в руб.). Примером логического высказывания может служить выражение
— зарплата респондента, измеренная по шкале отношений (в руб.). Примером логического высказывания может служить выражение 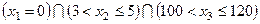 . Ясно, что каждое логическое высказывание задает определенную область рассматриваемого признакового пространства.
. Ясно, что каждое логическое высказывание задает определенную область рассматриваемого признакового пространства.
Разработанный Г. С. Лбовым подход к анализу исходных данных, полученных по разным шкалам, с успехом позволяет решать задачи, подобные описанным выше задачам поиска детерминирующих комбинаций значений признаков. А именно автор предлагает алгоритм, согласно которому при любом разбиении исходной совокупности объектов на классы (это разбиение может быть осуществлено, в частности, в соответствии со значениями некоторого зависимого, признака) для каждого такого класса может быть осуществлен поиск логических высказываний, выполняющихся (т.е. истинных) на принадлежащих ему объектах. (Выполнение понимается в некотором статистическом смысле. Грубо говоря, выполнение, высказывания для объектов какого-либо класса означает, что это высказывание истинно для большинства объектов этого класса.)
Но тот же подход позволяет решать и гораздо более широкий круг встающих перед социологом задач: задачу автоматической классификации исходных объектов (грубо говоря, в разные классы попадают объекты, для которых выполняются разные логические высказывания); задачу построения логических решающих правил, т. е. границ между классами, если задано, в какой класс каждый объект входит (такие правила также определяются в терминах логических высказываний); задачу динамического прогнозирования (алгоритм использует логические решающие правила.) и т. д.
Второй подход разработан группой исследователей под руководством Б. Г. Миркина[112]. Авторы этого подхода предлагают рассматривать каждый признак как некоторое отношение на множестве изучаемых объектов и задаватьего в виде булевой матрицы, т. е. матрицы, элементы которой могут принимать только два значения, например 0 и 1. Приведем пример.
Пусть для некоторых четырех респондентов заданы значения признаков: пол (0 — мужчина, 1 — женщина) и профессия {принимающая значения 1, 2, 3, 4) и пусть соответствующая матрица объект — признак имеет вид
| № респондента | Признак | |
| пол | профессия | |
Тогда рассматриваемым признакам будут соответствовать следующие булевы матрицы:
| № респондента | 1 2 3 4 | № респондента | 1 2 3 4 | |
| 1 1 0 1 1 1 0 1 0 0 1 0 1 1 0 1 | 1 0 0 0 0 1 0 0 0 0 1 1 0 0 1 0 |
На пересечении i-го столбца и j-й строки стоит единица, если значения рассматриваемых признаков для i-го и j-го объектов совпадают, и 0 — в противоположном случае.
Авторы рассматриваемого подхода предлагают основанные на использовании описанного способа представления исходных данных методы решения широкого круга задач, в том числе и социологических: классификация объектов, изучение связей между признаками, выявление латентных переменных и т. д. Например, в качестве латентного фактора, объясняющего связи между несколькими исходными признаками, заданными матрицами, подобны ми описанным выше, будет выступать признак, заданный матрицей, в определенном смысле близкой ко всем исходным матрицам одновременно (первым шагом решения соответствующей задачи будет поиск таких групп исходных матриц, для каждой из которых подобную среднюю матрицу можно найти).
Интересный подход к анализу структуры связей между рассматриваемыми переменными в тех случаях, когда эти переменные измерены по произвольным шкалам, предложен Ю. Н. Гаврильцом[113]. Этот подход позволяет учитывать, что связь может быть прямой и опосредованной, тесной и слабой и т. д., что изменение значений части признаков может менять характер распределения у другой части признаков, в то время как распределение третьей части признаков остается прежним. Основные принципы представления исходной информации, лежащие в основе этого подхода, являются слишком сложными для того, чтобы их можно было сформулировать в настоящем параграфе.
Последний подход к анализу информации, полученной по поминальной или порядковой шкале, о котором нам хотелось бы упомянуть,— это так называемая метризация используемых шкал (оцифровка значений признаков). Это — приписывание исходным шкальным значениям таких меток, чисел, что отношения между получающимися интервалами начинают иметь содержательный смысл. К настоящему времени разработано довольно много способов такого превращения номинальной либо порядковой шкалы в интервальную[114]. Однако использовать их надо с большой осторожностью, поскольку каждый из этих способов предполагает довольно сильные и часто трудно проверяемые свойства исходных шкальных значений (эти предположения могут быть как содержательными, таки формальными).
В заключение настоящего раздела отметим, что большинство описанных в этой главе методов реализовано в имеющихся в различных научных центрах нашей страны комплексах программ для ЕС ЭВМ. Методы дискриптивной статистики, вычисления, всевозможных мер связи, методы регрессионного анализа и другие методы многомерного статистического анализа, в том числе методы поиска детерминирующих характеристик значений независимых Примаков, реализованы в системе Социолог, применяемой в ИСИ АН СССР. Алгоритм поиска детерминационных характеристик, основанный на методе С. В. Чеснокова, представлен в системе, разработанной во ВНИИ системных исследований ГКНТ и АН СССР. Упомянутые выше алгоритмы, предложенные Г. С. Лбовым, реализованы- в пакете программ ОТЕКС Института математики СО АН СССР.
Литература для дополнительного чтения
1. Вайнберг Дж., Шумекер Дж. Статистика. М.: Статистика, 197?. 389 с.
2. Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии М.: Прогресс, 1976. 495 с.
3. Крамер Г. Математические методы статистики. М.: Мир, 1975. 648 с.
4. Лбов Г. С. Методы обработки разнотипных экспериментальных данных Новосибирск: Наука, 1981. 160 с.
5. Математические методы в социологическом исследовании/Отв. ред. Т. В. Рябушкин и др. М.: Наука, 1981. 332 с.
6. Миркин В. Г. Анализ качественных признаков и структур. М.: Статистика, 1980. 166 с.
7. Елисеева Ц. И., Рукавишников В. О. Группировка, корреляция, распознавание образов. М.: Статистика, 1977. 144 с.
8. Рунион Р. Справочник по непараметрической статистике, М.: Финансы и статистика, 1982. 198 с.
9. Рябушкин Т. В. Теория и методы экономической статистики. М.: Наука, 1977. 511 с.
10. Статистические методы анализа информации в социологических исследованиях/Отв. ред. Г. В. Осипов и др. М.: Наука, 1979. 319 с.
11. Типология и классификация в социологических исследованиях/Отв. ред. В. Г. Андреенков, Ю. Н. Толстова, М.: Наука, 1982. 296 с.
12. Тюрин Ю. Н. Непараметрические методы статистики. М.: Знание, 1978. 62 с.
ГЛАВА ШЕСТАЯ
ВЫБОРОЧНЫЙ МЕТОД В СОЦИОЛОГИЧЕСКОМ ИССЛЕДОВАНИИ
В марксистской социологии имеются давние традиции по применению методов статистического наблюдения. В настоящее время без них практически немыслимо проведение эмпирических социологических исследований.
В целом эти методы могут быть разделены на сплошные и не-сплошные. Сплошное статистическое наблюдение требует полного охвата объекта исследования, всех его элементов без исключения.
Сплошное исследование некоторых социальных объектов по многим причинам может оказаться или очень трудоемким, или требующим больших денежных затрат, или просто невозможным. В этих случаях используются методы несплошного наблюдения, которые очень хорошо себя зарекомендовали в различных областях науки и техники.
Строгому научно обоснованному выбору части социальных объектов как методу исследования всей совокупности большое значение .придавал В. И. Ленин. Он предлагал провести выборку для изучения небольшого числа типичных предприятий (фабрик, совхозов) и учреждений (a) наилучших, образцовых; (b) средних и ( 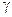 ) наихудших[115].
) наихудших[115].
Наиболее часто в социологии используются три метода несплошного наблюдения: 1. Монографический, 2. Метод основного массива, 3. Выборочный.
Монографический метод, строго говоря, выходит за рамки чисто статистического наблюдения, ибо наряду с фиксацией статистических данных предполагает детальное качественное описание массовых явлений. Выбираемая для монографического исследования часть объекта очень часто является типичной, в определенном смысле, для всего объекта или для важнейших его элементов.
Именно эта особенность, дающая возможность глубокого проникновения в сущность изучаемых массовых явлений, представляет важнейшее достоинство монографического метода, который, как правило, применяется в социологии в комбинации со сплошным или различными видами несплошного исследования.
Известно, например, какую роль В. И. Ленин отводил монографическому методу наблюдения за состоянием сельского хозяйства в нашей стране в целях его скорейшего подъема. В. И. Ленин выделял три группы крестьянских хозяйств по уровню их развития: «...поставленные заведомо хорошо, сносно и неудовлетворительно. Одно типичное хозяйство каждой из этих последних трех групп должно быть не менее двух раз в год описываемо подробно с точным указанием всех данных об описываемом хозяйстве»[116].
Значение монографического метода не ограничивается применением лишь к типичным объектам социологического исследования. Он оказывается весьма полезным при изучении объектов в социальном эксперименте, когда зарождается передовой опыт, намечаются ростки прогрессивных явлений.
Методом основного массива, как правило, изучается большая часть объекта социологического исследования или его важнейшие элементы. Этот метод находит применение, например, в некоторых социологических исследованиях, проводимых с помощью контент-аналиэа.
Разновидностью метода основного массива являются экспертные опросы, так как при организации таких опросов стараются привлечь большую часть наиболее компетентных экспертов.
Наиболее широкое распространение в социологических исследованиях получил выборочный метод. В этой главе подробно рассматривается суть этого метода и основные процедуры его применения в социологии.
1. Основные понятия выборочного метода
Генеральная и выборочная совокупности. Множество социальных объектов, которые являются предметом изучения в пределах, очерченных программой социологического исследования и территориально-временными границами, образует генеральную совокупность.
Любую генеральную совокупность характеризует некоторый явно задаваемый признак (или набор признаков), по значению которого всегда можно однозначно определить, относится данный объект к генеральной совокупности или нет. Так, в качестве генеральной совокупности мы можем рассматривать жителей данного города, промышленно-производственный персонал предприятия, студентов всей страны и т. п. Часть объектов генеральной совокупности, выступающих в качестве объектов наблюдения, называется выборочной совокупностью. Иными словами, если генеральная совокупность включает все без исключения единицы, составляющие объект исследования, то выборочная совокупность представляет собой специальным образом отобранную часть генеральной совокупности. При этом статистическое наблюдение осуществляется именно за элементами выборочной совокупности.
Внимательный читатель может заметить,, что метод основного массива и метод монографического исследования также предполагают статистическое наблюдение некоторой части исследуемой совокупности. В чем же характерный признак выборки? Выборочная совокупность обычно конструируется таким образом, чтобы при минимуме исследуемых объектов удавалось с необходимой степенью гарантии представить всю генеральную совокупность.
Единица отбора и единица наблюдения. Единицей отбора называют элементы генеральной совокупности, которые выступают единицами счета в различных процедурах отбора, формирующих выборку.
Единицами наблюдения называют элементы сформированной выборочной совокупности, которые непосредственно подвергаются статистическому наблюдению. Единица отбора и единица наблюдения представляют собой социальные объекты, обладающие характеристиками, существенными для предмета конкретного социологического исследования. Они могут совпадать (в простых схемах отбора) и различаться (при сложных комбинированных схемах отбора).
Систематические и случайные ошибки статистического наблюдения. При получении социальной информации выборочным методом могут возникать ошибки различного рода. Причинами могут быть неточность данных, сообщенных социологу респондентом, неправильная фиксация получаемых сведений или неправильное измерение переменных, характеризующих единицы наблюдения, и т. д. Эти ошибки, называемые иногда ошибками регистрации, могут быть разделены на два типа: случайные и систематические.
Систематической ошибкой регистрации называется ошибка, выражающая некоторые существенные связи, возникающие в процессе регистрации между объектом, субъектом и условиями проведения наблюдения. Систематическая ошибка может быть значительной по своей, величине из-за одностороннего искажения (в сторону увеличения или уменьшения) исследуемой характеристики. Происходящее вследствие этого накопление ошибки по исследуемой совокупности в целом может зачеркнуть результаты всего исследования.
Систематическая ошибка регистрации может возникнуть при любом типе статистического наблюдения, в том числе и при проведении выборочного или сплошного обследования.
Характерным примером систематической ошибки являются данные о женатых мужчинах и замужних женщинах во Всесоюзной переписи 1970 г. По результатам переписи в целом по Союзу .оказалось 53,0 млн. женатых мужчин и 54,2 млн. замужних женщин. Систематическая ошибка, зафиксированная в этой, переписи, образовалась из-за погрешностей в ответах, возникающих от различной оценки своего семейного положения мужчинами я женщинами.
Случайные ошибки регистрации отражают менее существенные связи между объектом, субъектом и условиями регистрации и складываются из различные статистических погрешностей в процессе наблюдения. Погрешности, имея различную направленность в отдельных единицах наблюдения, проявляют тенденцию к взаимному погашению при обобщении результатов .регистрации по всей исследуемой совокупности.
Таким образом, в отличие от систематической случайная ошибка вызывается при наблюдении причинами, носящими вероятностный характер.
Типичные ошибки выборочного социологического исследования. Ошибки регистрации встречаются при любом типе статистического наблюдения и, следовательно, свойственны и выборочному методу исследования.
Кроме того, в выборочном исследовании могут появиться ошибки, возникающие при различных отклонениях от планируемой выборки. Можно выделить два наиболее типичных вида отклонения от плана выборки.
1. Замена намеченных при планировании выборки единиц наблюдения другими, более доступными, которые, однако, оказываются неполноценными с точки зрения выработанного плана выборки.
Такого рода ошибки могут возникать при использовании- недостаточно квалифицированных интервьюеров. Например, опрос планируется провести в каждой десятой квартире жилого массива. Никого не застав в выбранных квартирах, интервьюер иногда обращается в соседние квартиры и берет интервью. В итоге в выборке оказывается значительная доля пенсионеров, больших по размеру семей и слабо представлены одинокие лица и малочисленные семьи. Ошибок этого типа (ошибок подстановки) можно избежать, контролируя деятельность анкетеров и интервьюеров и качество собранной ими информации. В противном случае они могут привести к серьезным систематическим ошибкам.
2. Неполный охват выборочной совокупности, т. е. неполучение информации от части единиц наблюдения, включенных в выборку (например, недополучение почтовых анкет, не полностью заполненные анкеты).
Эти ошибки устанавливаются путем сравнения реально сформированной выборки с ее планом. Ошибки подобного рода снимаются так называемой процедурой корректировки выборки, т. е. путем специального пересчета значений изучаемого признака с учетом того, какая именно часть выборочной совокупности выпала из обследования.
Распространенными ошибками в выборочном социологическом исследовании являются ошибки, возникающие при неправильной разработке плана выборки. Только правильно намеченный и, конечно, реализованный план формирования выборочной совокупности может дать определенные гарантии, для распространения выводов, полученных по выборке, на всю генеральную совокупность.
Во многих книгах в качестве примера смещения, возникающего из-за неправильного планирования выборки, приводится известный опрос, проведенный Литэрари Дайджест (Литературное обозрение) относительно исхода президентских выборов 1936 г. в США.
Кандидатами на этих выборах были Ф. Д. Рузвельт и А. М. Лан-дон. Редакция журнала организовала план выборки следующим образом. В выборку попали более двух миллионов американцев, выбранных при помощи случайного отбора из списков, имеющихся в телефонных книгах. По всей стране попавшим в выборку лицам были разосланы открытки с просьбой назвать фамилию будущего президента. Затратив огромную сумму на рассылку, сбор и обработку полученных открыток, журнал информировал общественность, что на предстоящих выборах президентом США с большим перевесом будет избран А. М. Ландон. Результаты выборов опровергли этот прогноз.
В то же время социологи Д. Гэллап и Э. Роупер правильно предсказали победу Ф. Д. Рузвельта, основываясь только на четырех тысячах анкет.
Ошибочный прогноз относительно возможного президента объясняется неправильным планом выборки, который не обеспечил полного отражения в ней всей генеральной совокупности: в телефонных книгах, которые использовались для организации выборки, были представлены лишь наиболее обеспеченные слои американского населения, в частности домовладельцы. Поскольку обеспеченные слои американцев составляют меньшую часть генеральной совокупности, то распространение мнения этой части населения на всю страну в целом оказалось ошибочным.
Ошибки часто возникают и в тех случаях, когда в выборочную совокупность преимущественно попадают представители одинаковых социальных групп. Так, почтовые анкеты чаще заполняют лица с более высоким уровнем образования, причем мужчины чаще, чем женщины, пенсионеры чаще, чем работающие и т. д.
Социолог самое пристальное внимание должен уделять анализу возможностей возникновения ошибок смещения в выборочных социологических исследованиях.
Репрезентативность выборки. Выборка в определенном смысле должна быть моделью генеральной совокупности, что и позволяет на ее основе оценивать характеристики этой совокупности. Однако нет необходимости моделировать в выборке все аспекты генеральной совокупности, достаточно лишь значимых с точки зрения задач исследования. Свойство выборки отражать, моделировать эти характеристики будем называть репрезентативностью.
Основной принцип построения выборки (точнее, вероятностного отбора) состоит в том, чтобы обеспечить всем элементам генеральной совокупности равные шансы попасть в выборку. Однако даже самое аккуратное соблюдение этого принципа не гарантирует выборку от искажений. Эти искажения — случайные ошибки — внутренне присущи выборочному методу. Они появляются в результате .того, что обследуются не все единицы совокупности, а только выборка, и, следовательно, результат будет неточен, так как единицы совокупности не тождественны между собой. Значение случайной ошибки можно сравнительно легко вычислить, используя аппарат, разработанный в статистической теории выборочного метода. Таким образом, репрезентативность выборки будет определяться двумя компонентами: ошибками регистрации и случайными ошибками.
В идеальной ситуации в сплошном исследовании отсутствуют ошибки репрезентативности, благодаря чему при правильной организации наблюдения ошибка выборочного исследования больше ошибки наблюдения при сплошном обследовании. Однако в социологии применение сплошного обследования требует значительного числа анкетеров и интервьюеров, а это ведет к тому, что иногда привлекаются недостаточно квалифицированные кадры, участие которых в исследовании увеличивает ошибку регистрации. И наоборот, применение выборочного исследования при решении, тех же вопросов позволяет использовать более подготовленные кадры специалистов, обеспечить лучший их инструктаж, контроль за его выполнением. Это ведет к уменьшению ошибки регистрации. И если случайная ошибка не велика, то ошибка выборочного наблюдения в целом может оказаться меньше ошибки сплошного исследования. Таким образом, при определенных условиях выборочный метод оказывается более точным, чем сплошной, что еще раз подчеркивает его преимущество при организации и проведении эмпирических социологических исследований.
2. Простой случайный отбор
Основа выборки. Для организации простых схем отбора (простой случайной, систематической или серийной выборок) необходима информация обо всех элементах генеральной совокупности или хотя бы их перечень.
Основой выборки называют перечень элементов генеральной совокупности, если он удовлетворяет требованиям полноты, точности, адекватности, удобства работы с ним, отсутствия дублирования единиц наблюдения. Основой могут служить алфавитные списки сотрудников учреждения, номера, пропусков, по которым можно идентифицировать определенные единицы, и т. п.
Полнота. Под полнотой подразумевается представленность всех единиц данной генеральной совокупности в основе выборки. Если некоторые единицы, которые по предположению должны быть в списке, незарегистрированы в нем, то список является неполным.
Неполнота основы выборки приводит к серьезным ошибкам в том случае если не включенные в выборочную совокупность единицы наблюдения имеют существенные особенности и их достаточно много.
Отсутствие дублирования. Если некоторые единицы наблюдения генеральной совокупности будут включены в основу выборки более чем один раз, то они могут повторяться и в выборке (например, в том случае, когда человек переезжает из одного района в другой и включается в новый список раньше, чем исключается из старого).
Точность. Информация о каждой единице отбора должна быть точной. Основа выборки не должна содержать несуществующих единиц. Подобные неточности встречаются в избирательных списках, когда отсутствуют вновь прибывшие в данный населенный пункт, или остаются лица, изменившие свое местожительство, умершие, жильцы снесенных домов и т. п.
Адекватность. Основа выборки, адекватная для решения одних задач, может быть неадекватной для других. Например, полный список работников промышленного предприятия может быть хорошей основой для формирования выборочной совокупности при исследовании проблем удовлетворенности трудом работников данного предприятия, уровня их социальной активности и т. д. Но если изучается удовлетворенность трудом или социальная активность и т. д. не всех работников предприятия, а только молодежи, то- этот -полный список может послужить лишь для формирования новой основы выборки — списка молодежи.
Если основа охватывает не все социальные объекты генеральной совокупности, то она может использоваться как основа выборки для той части генеральной совокупности, которая представлена полностью, а выбор единиц наблюдения из остальной части следует организовать по другим источникам.
Удобство. Удобство работы с основой выборки—существенное условие повышения качества результатов. Удобно, когда единицы составляющие основу выборки, пронумерованы, когда имеющиеся сведения о них дают возможность с полной определенностью опознавать эти единицы. Если основа выборки находится в одном централизованном месте и ее структура соответствует реальной структуре изучаемых социальных объектов, это не только облегчает работу социолога, но и является необходимым требованием к исследованию,. значительно повышающим его качество.
Одной из причин возникновения сложных схем выборки (многоступенчатых, комбинированных и т. п.) является невозможность обеспечить основу выборки для очень больших генеральных совокупностей, обладающих сложной структурой.
К настоящему времени сложились представления об основе, которая могла бы удовлетворить требованиям организации современных социологических исследований, быть действенной для различного типа исследований. Такой основой является социальная карта.
Социальная карта. Подобно тому как географическая карта является ориентиром в пространственном движении, социальная карта должна стать ориентиром в исследовании социальных объектов. Социальная карта представляет собой пространственное распределение всевозможных социальных показателей для определенных экономико-географических регионов. Такая карта может служить основой всех выборочных исследований- в каждом регионе, области,, районе, городе и т. п.
Процесс составления социальной карты складывается из следующих этапов.
1. Сбор информации о размещении и движении населения, обоснованных постоянных и сезонных потоках населения, которые выражаются в демографических показателях.
2. Сбор социально-экономической информации относительно профессионального состава населения: данные о квалификации, заработной плате, соотношения между работающими и неработающими, распределение уровня семейных доходов и т. д.
3. Сбор социологической информации: условия труда и быта; данные о проведении досуга, о его структуре по различным социальным группам; данные о различных формах социальной активности, образовательном уровне, средствах, массовой коммуникации, об активности партийных и общественных организаций и т. д.
Возрастающий интерес социологов к построению социальных парт связан в значительной степени с прикладными задачами выборочного обследования. Для более углубленной разработки социальных проблем необходима и более основательная исходная социальная информация: карта размещения социальных групп, распространенности средств массовых коммуникаций и т. д., т. е. социальная, карта.
Процедура простого случайного отбора. По сформированной основе выборки легко реализовать процедуру простого случайного отбора. Для этого требуется соблюдение равенства шансов попадания единиц отбора в выборочную совокупность. Выделяют: а) простой случайный бесповторный отбор и б) простой случайный повторный отбора.
Осуществляться каждая из разновидностей процедуры может различными способами. Опишем один из них. Пусть основа выборки содержит N единиц. Тогда, чтобы выбрать п единиц наблюдения в выборочную совокупность, напишем все номера от 1 до N на отдельные карточки, тщательно их перемешаем и наугад вынем одну -из них. Номер вытащенной карточки задает соответствующую единицу наблюдения, попавшую в выборочную совокупность. Затем карточка возвращается на место, они снова перемешиваются, наугад вынимается новая карточка, и так далее продолжается п раз. Таи реализуется процедура простого случайного повторного отбора.
Дата добавления: 2015-09-29; просмотров: 883;
