Коэффициенты взаимозависимости для номинального уровня измерения. 1 страница
Связь в табл. 2×2. Простейшая задача о взаимозависимости возникает тогда, когда имеются два признака, каждый из которых принимает два значения (табл. 13).
Таблица 13. Распределение отношения к правилам уличного движения в зависимости от пола
| Отношение к правилам уличного движения в течение месяца, % | Пол | Всего | |
| мужской | женский | ||
| Нарушение Соблюдение | |||
| Всего |
Представим данные о группировке по этим двум признакам так:
| В | не В | Сумма | |
| А Не А | a c | b d | a + b c + d |
| Сумма | a + c | b + d | n (либо 100%) |
Для характеристики степени связи двух признаков применяется коэффициент Ф, определяемый формулой
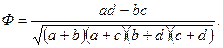 (42)
(42)
Коэффициент Ф равен 0, если нет соответствия между двумя дихотомическими переменными, и равен 1 или —1, когда имеется полное соответствие между ними. В силу трудностей с интерпретацией знака коэффициента для категоризованных (номинальных) переменных часто используют в анализе лишь абсолютную величину — 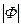 . Ф легко интерпретируется, поскольку показано, что он представляет собой просто коэффициент корреляции r, если значения каждой дихотомической переменной обозначить 0 и 1.
. Ф легко интерпретируется, поскольку показано, что он представляет собой просто коэффициент корреляции r, если значения каждой дихотомической переменной обозначить 0 и 1.
Как уже отмечалось, Ф вычисляется для категоризованных данных, представляющих естественные дихотомии: пол, раса, и т. п. Приведение количественных переменных к дихотомическому виду связано с выбором граничной точки разделения (например, мужчины до 30 лет и мужчины старше 30 лет). Искусственная дихотомизация, столь часто необходимая в конкретном исследовании при изучении взаимосвязи признаков, может привести к тому, что одна часть дихотомической переменной по своему воздействию будет более значима для одной связи, другая— для другой, а это даст ошибочный результат.
Измерение связи в табл., с×k. Рассмотрим теперь более общую ситуацию, когда две переменные классифицированы на две или более категории. Запишем это таким образом:
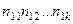
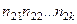 ……………
……………
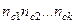
| 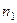
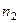 ….
….
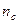
|
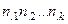
|
где 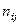 частоты;
частоты; 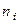 — маргинальные суммы частот по строкам;
— маргинальные суммы частот по строкам; 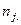 — маргинальные суммы частот по столбцам. На с. 169 — 172 для выяснения отклонения от независимости распределения значений в подобном случае использовался критерий
— маргинальные суммы частот по столбцам. На с. 169 — 172 для выяснения отклонения от независимости распределения значений в подобном случае использовался критерий 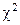 . Однако сама величина
. Однако сама величина 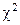 не очень подходит в качестве меры связи, поскольку сильно зависит от числа категорий.
не очень подходит в качестве меры связи, поскольку сильно зависит от числа категорий.
Нормированным коэффициентом корреляции для таблицы с×k является коэффициент сопряженности Пирсона (Р):
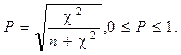 (43)
(43)
Коэффициент Р = 0 при полной независимости признаков. Недостатком его является зависимость максимальной величины Р от размера таблицы (максимум Р достигается при, с = k, но сама граница изменяется с изменением числа категорий). В связи с этим возникают трудности сравнения таблиц разного размера.
Чтобы исправить указанный недостаток, Чупров ввел другую величину:
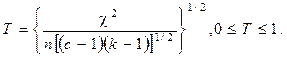 (44)
(44)
При с = k Т достигает +1 в случае полной связи, однако не обладает этим свойством при 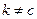 .
.
Коэффициент Крамера (К) может всегда достигать +1 независимо от вида таблицы:
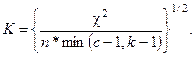 (45)
(45)
Для квадратной таблицы коэффициенты Крамера и Чупрова совпадают, а в остальных случаях К>Т.
Величина 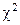 быстро вычисляется с помощью формулы
быстро вычисляется с помощью формулы
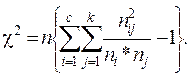
Вычисление коэффициентов Р, Т и К связано с теми же ограничениями на 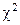 , которые сформулированы на с. 172.
, которые сформулированы на с. 172.
Следующая группа коэффициентов связи для категоризованных данных основана на предположении, что если две переменные связаны, то информация об одной переменной может быть использована для предсказания другой. Так, если предположить, что связь между полом индивида и его отношением к правилам уличного движения абсолютно детерминирована, то согласно табл. 13 либо все мужчины были бы нарушителями, а женщины нет, либо наоборот. Поскольку это но так, то возникает несоответствие, или, как говорят, ошибка предположения абсолютной связи (обозначим величину этой ошибки ОА).
С другой стороны, можно предположить, что два признака абсолютно не связаны, и нельзя на основе одной переменной предсказать другую. Поскольку это тоже не так, то возникает ошибка предположения об отсутствии связи (О0).
Тогда величина 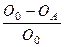 может служить мерой относительного уменьшения ошибки при использовании информации об одной переменной для предсказания другой.
может служить мерой относительного уменьшения ошибки при использовании информации об одной переменной для предсказания другой.
Признак, на основе которого предсказывается другой признак, будем называть независимой переменной, а предсказываемый — зависимой.
Тогда для случая, когда зависимая переменная расположена по строкам таблицы (т. е. категории расположены по строкам), вычисляется коэффициент связи 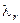 :
:
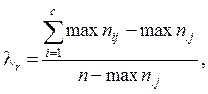 (47)
(47)
где 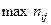 — наибольшая частота в столбце i;
— наибольшая частота в столбце i; 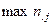 — наибольшая маргинальная частота для строк j.
— наибольшая маргинальная частота для строк j.
Пример. Вычислим 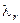 для данных табл. 13 в предположении, что пол независимая переменная, а отношение к правилам уличного движения — зависимая
для данных табл. 13 в предположении, что пол независимая переменная, а отношение к правилам уличного движения — зависимая
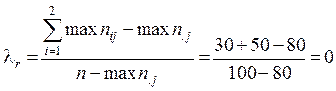
Таким образом, использование информации о поле обследованных для предсказания отношения к правилам движения не уменьшает относительной ошибки.
Если зависимая переменная — это категории столбцов таблицы, то совершенно аналогично предыдущему вычисляется
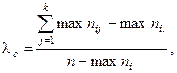 (48)
(48)
где 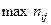 — наибольшая частота в строке j;
— наибольшая частота в строке j; 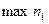 — наибольшая маргинальная частота для столбцов i.
— наибольшая маргинальная частота для столбцов i.
Для нашего примера, когда пол зависимая переменная, 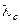 = 0,4, т. е. получаем 40%-ное уменьшение в ошибке, если используем отношение к правилам в качестве предсказывающей пол нарушителя.
= 0,4, т. е. получаем 40%-ное уменьшение в ошибке, если используем отношение к правилам в качестве предсказывающей пол нарушителя.
Коэффициенты 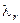 и
и 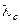 имеют пределы изменения от 0 до 1. Чем ближе
имеют пределы изменения от 0 до 1. Чем ближе 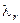 или
или 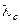 к 1, тем больше относительное уменьшение в ошибке и большее соответствие (связь) между переменными. Эти коэффициенты могут быть использованы для таблиц любого размера.
к 1, тем больше относительное уменьшение в ошибке и большее соответствие (связь) между переменными. Эти коэффициенты могут быть использованы для таблиц любого размера.
В ряде случаев удобно использовать симметричную 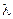 ;
;
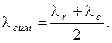 (49)
(49)
Разнообразие корреляционных коэффициентов продиктовано стремлением отразить реально существующее разнообразие типов связей в природе и обществе. Поэтому данное обстоятельство следует рассматривать скорее как свидетельство достоинств статистического аппарата, заключающихся в гибкости и большой приспособленности его к анализу сложнейших взаимосвязей в социальной области. Каждый корреляционный коэффициент приспособлен для измерения вполне определенного вида связи. Техника расчета и конструкция формулы одного и того же коэффициента могут измениться в зависимости от того, какие (например, сгруппированные или несгруппированные) данные приходится анализировать. Сравните, например, различные варианты формул для парного коэффициента корреляции r. Таким образом, применение того или иного показателя определяется природой данных и формой их представление. Требуемая степень точности также может существенно повлиять па выбор способа расчета связи в каждом конкретном случае. Обычно оценка пригодности той или иной формулы производится с учетом следующих факторов:
1) природы данных (качественные или количественные признаки);
2) формы и типа зависимости (линейная или нелинейная, положительная или отрицательная связь);
3) требуемой точности расчетов (например, коэффициенты корреляции рангов 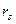 и
и 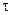 иногда могут использоваться вместо более точных мер r и
иногда могут использоваться вместо более точных мер r и 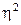 );
);
4) удобства - при вычислении и сравнительной простоты интерпретации; .
5) трудностей технического порядка (имеется ли счетная техника или нужно вести расчеты вручную);
6) распространенности использования того или иного коэффициента корреляции;
7) возможности сравнения различных коэффициентов. Обычно предпочитают использовать наиболее распространенные в практике социологических исследований коэффициенты, так как тем- самым достигается возможность сравнения полученных результатов с материалами других исследований.
7. Новые подходы к анализу данных, измеренных по порядковым и номинальным шкалам
В последние годы как у нас в стране, так и за рубежом разработано довольно много математических методов, предназначенных для анализа данных, полученных с помощью измерения по номинальным и порядковым шкалам. Однако многие из них малознакомы широкому кругу социологов. В настоящем параграфе представлен краткий обзор таких методов. К сожалению, в силу сложности и большого объема материала нет возможности подробно изложить суть каждого метода и тем более описать конкретную методику его применения. Поэтому все излагаемое ниже можно рассматривать лишь как некоторое указание на то, к какой литературе необходимо обратиться для решения соответствующей задачи и какого рода вопросы необходимо поставить в этой связи перед математиком.
Наиболее распространенными задачами, при решении которых исследователь прибегает к помощи математических методов, являются задачи изучения связей между признаками, нахождения латентных переменных, классификации объектов.
Рассмотрим задачу изучения связей между признаками. В предыдущем разделе этой главы уже рассматривались меры связи между номинальными признаками, основанные на анализе таблиц сопряженности. Определенного рода обобщением способов измерения таких связей с помощью критерия 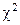 можно считать метод логлинейного анализа частотных таблиц. В отличие от упомянутых мер связи логлинейный анализ позволяет анализировать таблицы сопряженности любой размерности и проверять гипотезы о наличии сложных структур связи, состоящие из предположений о существовании связей внутри жаждой из нескольких групп признаков одновременно. Принципы логлинейного анализа описаны в литературе достаточно подробно[99].
можно считать метод логлинейного анализа частотных таблиц. В отличие от упомянутых мер связи логлинейный анализ позволяет анализировать таблицы сопряженности любой размерности и проверять гипотезы о наличии сложных структур связи, состоящие из предположений о существовании связей внутри жаждой из нескольких групп признаков одновременно. Принципы логлинейного анализа описаны в литературе достаточно подробно[99].
В основе традиционных подходов к измерению связей между номинальными признаками лежит представление о последней как об интегральной, т. е. о связи между рассматриваемыми признаками в целом (при расчете меры связи учитываются одновременно все те значения, которые эти признаки могут принимать). Однако такое понимание связи не является единственно возможным. Она может пониматься и как локальная, т. е. как связь между отдельными значениями (одним или несколькими рассматриваемыми признаками). Наличие интегральной связи отнюдь не означает наличия локальной, и наоборот. Так, вывод об отсутствии интегральной связи между полом и курением (например, основанный на малой величине 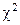 может не подтвердиться на основе локального анализа той же таблицы данных: т. е. можно предположить, что свойство респондента быть мужчиной довольно жестко определяет то, что этот человек курит (свойство быть женщиной в этом смысле может быть не связано с курением).
может не подтвердиться на основе локального анализа той же таблицы данных: т. е. можно предположить, что свойство респондента быть мужчиной довольно жестко определяет то, что этот человек курит (свойство быть женщиной в этом смысле может быть не связано с курением).
В настоящее время разработан довольно широкий круг методов анализа описанных локальных связей. В литературе они часто называются методами поиска детерминирующих комбинаций значений переменных (или взаимодействий последних)[100]. Прежде чем подробнее пояснить суть задачи и подходы к ее решению, введем некоторые обозначения.
Пусть изучается влияние каких-то l признаков (переменных), обозначаемых ниже 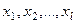 на некоторый интересующий исследователя признак у. Признаки
на некоторый интересующий исследователя признак у. Признаки 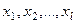 будем называть независимыми переменными, а признак у — зависимой переменной. Поясним, что имеется в виду под задачей поиска детерминирующих комбинаций значений переменных.
будем называть независимыми переменными, а признак у — зависимой переменной. Поясним, что имеется в виду под задачей поиска детерминирующих комбинаций значений переменных.
Исследователь полагает, что рассматриваемые независимые признаки в определенной степени обусловливают тип поведения изучаемых объектов, проявляющийся в том, какие значения для того или иного объекта может принимать зависимая переменная. Другими словами, выдвигается гипотеза о соответствующей детерминации (типа поведения сочетаниями значений не зависимых переменных).
Упомянутый тип поведения может пониматься по-разному. Например, его можно определить как указание вероятностей, с которыми объект, обладающий заданным сочетанием значений х, имеет то или иное значение у. В таком случае тип поведения фактически отождествляется с распределением значений зависимого признака для объектов, имеющих рассматриваемый набор значений независимых признаков. Например, если при решении упомянутого .выше вопроса о связи пола-респондента с привычкой к курению придем к выводу, что для мужчин вероятность иметь такую привычку равна 0,8, а не иметь ее — 0,2 и что для женщин аналогичные вероятности равны соответственно 0,3 и 0,7, то будем иметь основания говорить о двух типах поведения респондентов, каждый из которых определяется полом последних.
Можно тип поведения отождествить со средним арифметическим множества значений зависимой переменной для рассматриваемой совокупности объектов (в таком случае естественно предполагать, что значения у получены ]по интервальной шкале). Пусть, например, у — это время, затрачиваемое респондентом в течение дня на чтение газет, 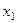 — под респондента,
— под респондента, 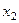 — его образование. Если в процессе исследования мы обнаружим, что мужчины с высшим образованием тратят на чтение газет в среднем 1,5 часа в день, а женщины с начальным образованием — 0,01 часа, то можно будет говорить о двух типах поведения респондентов, каждый из которых соответствующим образом связан с рассматриваемыми независимыми признаками.
— его образование. Если в процессе исследования мы обнаружим, что мужчины с высшим образованием тратят на чтение газет в среднем 1,5 часа в день, а женщины с начальным образованием — 0,01 часа, то можно будет говорить о двух типах поведения респондентов, каждый из которых соответствующим образом связан с рассматриваемыми независимыми признаками.
Тип поведения объекта можно отождествить и с тем, что для этого объекта у принимает определенное значение. Подчеркнем, что в любом случав упомянутая выше гипотеза о детерминации не может означать предположения о «жестком» определении значения по сочетанию значений х.
В соответствии с выдвинутой гипотезой исследователь ставит перед собой задачу выяснить, какие именно сочетания значений независимых признаков являются в интересующем его смысле детерминирующими (определяющими тип поведения объектов). Иногда к этому добавляется и задача выделения из числа независимых переменных подсовокупности признаков, наиболее информативных в том смысле, что по сочетанию именно их значений с наибольшей степенью уверенности можно судить о типе поведения объектов. В едином комплексе с этими задачами может решаться и задача выявления самих типов поведения, свойственных объектам изучаемой совокупности. Именно сочетание названных трех задач (может быть, без второй или третьей) и называется задачей поиска детерминирующих комбинаций значений переменных.
В соответствии с тем, как понимается тип поведения объектов, должен формироваться критерий, является ли тот или иной набор сочетаний значений х детерминирующим это поведение. Многообразие методов поиска детерминирующих характеристик и объясняется в основном различием таких критериев.
Например, первому описанному выше пониманию типа поведения отвечает поиск такого разбиения исходной совокупности объектов (соответствующего определенному набору сочетаний значений х), что каждой выделенной подсовокупности будет соответствовать свое распределение значении у (степень различия распределений определяется в соответствии с известными статистическими критериями). Искомые детерминирующие комбинации — это те наборы сочетаний значений с, которые соответствуют выделенным подсовокупностям[101].
Второму пониманию типа поведения отвечает поиск такого разбиения исходной совокупности объектов, при котором каждая подсовокупность будет иметь свое среднее арифметическое значение у (т. с. разница между соответствующими средними значениями будет статистически значима)[102]. Отметим тесную связь такого подхода с методами дисперсионного анализа. С помощью которого можно изучать влияние совокупности качественных признаков па некоторый количественный признак[103]. Однако дисперсионный анализ предназначен для изучения интегральных связей. Он исходит из априори заданных групп объектов — каждая группа соответствует одному возможному сочетанию значений независимых переменных и позволяет проверить гипотезу о совпадении типов поведения этих групп (тип поведения в дисперсионном анализе понимается именно рассматриваемым образом). Описываемые же нами методы решают более широкую задачу — они позволяют проанализировать с той же точки зрения все возможные группы объектов, соответствующие тому или иному набору сочетаний значений независимых переменных.
Подчеркнем, что при использовании описанных подходов ищутся не только сочетания значений независимых переменных, определяющих некоторые типы поведений, но и сами эти типы.
Для иллюстрации одного из возможных подходов к поиску детерминирующих комбинаций значений переменных при третьем упомянутом выше понимании типа поведения дадим некоторые определения, введенные С. В. Чесноковым[104], и приведем пример из его же работы. Привлекательность методики поиска детерминирующих характеристик, предложенной этим автором, в том, что она по существу является формализацией рассуждений, наиболее часто использующихся социологом при практическом решении задач о статистической зависимости.
Рассмотрим случай, когда данные представлены таблицей 2×2, изучаемые объект —респонденты, признак х принимает значения а и b, а признак у — значения с и d. Назовем типом поведения респондента соответствующее ему значение у и ниже будем говорить о детерминации значением а типа поведения с. Очевидно, считать, что такая детерминация действительно имеет место, можно только в том случае, если достаточно велика степень уверенности в реализации поведения с для объекта, со значением а независимой переменной. Уточним смысл такой уверенности.
Назовем интенсивностью детерминации а®с величину I(а®с), равную доле респондентов, для которых у = с в группе респондентов, удовлетворяющих условию: х = а. Интенсивность детерминации означает точность высказывания «если а, то с». Назовем емкостью детерминации а®с величину c(а®с), равную доле респондентов, для которых х = а, в группе респондентов, удовлетворяющих условию у = с. Емкость детерминации измеряет долю случаев реализации поведения с, которая объясняется высказыванием из в следует. Емкость c(а®с) отражает, насколько всеобъемлюще объяснение, построенное на детерминации (а®с), т. е. полноту этой детерминации.
Для обоснованности выводов о том, что «а влечет с», недостаточно знать I, необходимо оценить и С.
Пример. Пусть х — пол (а — мужчина, b — женщина), а у — величина зарплаты (с—высокая, d — низкая). Предположим, что частотная таблица имеет вид
| y | x | |
| мужчины (a) | женщины (b) | |
| Высокая зарплата (c) Низкая зарплата (d) |
Тогда очевидно, что
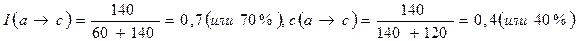
На основании того, что 70% мужчин имеют высокую зарплату, мы не можем говорить, что пол детерминирует величину зарплаты. Для этого вывода необходимо еще оценить, какова доля мужчин среди лиц с высокой зарплатой. Например, если этот процент равен I, то сформулированный вывод вряд ли можно считать справедливым. Полученные же в рассматриваемом примере 40% могут способствовать обоснованию этого вывода; если исследователь сочтёт этот процент достаточно высоким.
Показатели, аналогичные введенным величинам I и С, легко можно определить и для того случая, когда количество независимых признаков более одного.
Очевидно, в отличие от тех ситуаций, когда тип понимается одним из двух описанных выше способов, в данном случае мы не выявляем типы поведения в процессе нахождения детерминирующих сочетаний. Такая задача решается отдельно для каждого значения зависимой переменной: фиксируя это значение (т. е. тип поведения), мы ищем такие сочетания значений независимых переменных, которые определяют его с достаточно высокими значениями I и С (смысл выражения достаточно высокие определяется исследователем).
Наряду с методами поиска детерминирующих комбинаций значений переменных разработаны подходы к выявлению связей между номинальными признаками, аналогичные методам регрессионного анализа. В последнее десятилетие был предложен ряд подходов к решению этого вопроса[105]. Опишем один из них.
Прежде всего заметим, что если все рассматриваемые переменные дихотомические, то, применяя к исходным данным технику обычного регрессионного анализа, будем получать содержательно интерпретируемые результаты[106]. Это связано с тем, что дихотомическую шкалу можно считать частным случаем интервальной. Приведем пример вычисления регрессионной зависимости между номинальными переменными, в котором реализуется метод, основанный на сделанном замечании.
Сначала каждая переменная, принимающая I значений, заменяется на I фиктивных дихотомических переменных: каждому исходному значению соответствует своя дихотомическая переменная.
Пусть 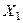 и
и 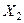 — исходные независимые номинальные переменные, принимающие каждая три значения — 1, 2, 3. Через
— исходные независимые номинальные переменные, принимающие каждая три значения — 1, 2, 3. Через 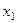 ,
, 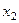 ,
, 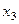 ,
, 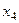 ,
, 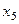 ,
, 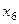 обозначим вводимые фиктивные переменные (
обозначим вводимые фиктивные переменные ( 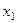 ,
, 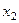 ,
, 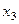 соответствуют переменной
соответствуют переменной 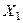 ,а
,а 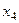 ,
, 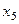 ,
, 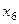 —
— 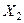 ). Значения, принимаемые фиктивными переменными, можно понять из следующей таблицы, где приведены значения
). Значения, принимаемые фиктивными переменными, можно понять из следующей таблицы, где приведены значения 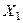 и
и 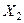 для некоторых трех объектов.
для некоторых трех объектов.
| № объекта | Значение исходных переменных | Значение фиктивных переменных | |
| 0 1 0 1 0 0 1 0 0 0 0 1 0 0 1 0 1 0 | |||
К полученным фиктивным переменным применяется обычная техника регрессионного анализа. Причем, поскольку зависимая переменная также заменена на k фиктивных переменных (если она принимает k значений), вместо одного уравнения рассчитывается k уравнений: для каждой упомянутой фиктивной переменной строится свое уравнение регрессии. Для оценивания влияния независимых переменных на зависимую в целом (а не на отдельные соответствующие ей фиктивные переменные) служит комплекс различных коэффициентов.
Аналогичный подход можно использовать и в случае, если зависимая переменная получена по интервальной шкале[107].
Как уже отмечалось, помимо задачи анализа связей между переменными, довольно актуальными для социологии являются также задачи нахождения латентных переменных и классификации объектов. Правда, эти задачи очень часто можно рассматривать как частный случай задачи изучения связей: латентные факторы обычно находятся именно на основе анализа связей между наблюдаемыми признаками, а для осуществления классификации, как правило, анализируются связи между объектами. Но тем не менее названные задачи -имеют и свою специфику, обусловленную их ролью в изучении интересующих социолога вопросов. Это обусловливает и определенную специфику соответствующих математических методов. Поэтому имеет смысл сказать несколько слов о путях решения обеих задач, когда изучаемые объекты характеризуются значениями номинальных или порядковых признаков[108].
Поиск латентных переменных может осуществляться с помощью методов латентно-структурного анализа. Кроме того, возможны различные подходы к использованию традиционных методов факторного анализа для анализа данных, полученных по порядковой и номинальной шкалам[109].
Основная проблема, встающая перед исследователем, желающим применить математические методы классификации к объектам, заданным значениями номинальных и порядковых признаков, — это проблема выбора меры близости между этими объектами. Большинство традиционных мер рассчитано на признаки, измеренные по интервальной шкале. Однако известны и такие меры, которые могут быть применены в интересующем нас случае. Выбор подходящей меры близости обеспечивает возможность использования многих методов классификации[110].
Далее рассмотрим несколько разработанных советскими авторами общих подходов к задаче анализа качественных данных.
Дата добавления: 2015-09-29; просмотров: 1456;
