СХЕМА 3 4 страница
Существует ряд упрощенных приемов вычисления средних. На с. 163 как промежуточный этап рассмотрено вычисление среднего методом отсчета от условного нуля.
Пример. Вышеприведенные данные о количестве прочитанных газет сгруппируем следующим образом:
| Номер опрошенного i | 1 10 | 2 3 5 7 | 4 8 9 | ||
| Число читаемых газет xi | 3 3 | 4 4 4 4 | 5 5 5 | ||
| Частота ni | 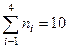
| ||||
Отсюда вычислим  : :
 (газеты) (газеты)
|
Медиана. Медианой называется значение признака у той единицы совокупности, которая расположена в середине ряда частотного распределения.
Если в ряду четное число членов (2k), то медиана равна среднему арифметическому из двух серединных значений признака. При нечетном числе членов (2k+1) медианным будет значение признака у (k + 1) объекта.
Предположим, что в выборке из 10 человек респонденты проранжированы по стажу работы на данном предприятии:
| Ранг опрошенного | ||||||||||
| Стаж |
Серединные ранги 5 и 6, поэтому медиана равна
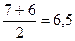 лет
лет
В интервальном ряду с различными значениями частот вычисление медианы распадается на два этапа: сначала находят медианный интервал, которому соответствует первая из накопленных частот, превышающая половину всего объема совокупности, а затем находят значение медианы по формуле
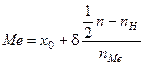 , (2)
, (2)
где x0 — начало (нижняя граница) медианного интервала; d — величина медианного интервала;  — сумма частот (относительных частот) интервалов; nH — частота (относительная), накопленная до медианного интервала; nMe — частота (относительная) медианного интервала.
— сумма частот (относительных частот) интервалов; nH — частота (относительная), накопленная до медианного интервала; nMe — частота (относительная) медианного интервала.
Проведем вычисление по данным табл. 2, где в нижней строке приведены накопленные относительные частоты. Первая из них превышающая половину совокупности (100/2 = 50%), равна 57,9% Следовательно, медиана принадлежит интервалу 3—4 года. Поэтому

Таким образом, для данной выборки медиана, равная 3,7 года, показывает, что 50% семей имеют соотношение возрастов, меньше этой величины, а другие 50% — большее. Медиана, может быть легко определена графически по кумуляте распределения (см. рис. 3).
Медиана может быть применена для дискретных переменных, хотя дробные значения, часто не имеют непосредственной содержательной интерпретации.
По данным распределения рабочих по тарифным разрядам (см. с. 156) вычислим медиану этого распределения, используя приведенную выше формулу[86]. Получим
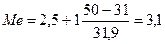
Узнали, что 50% рабочих имеют разряд, меньший 3,1, и 50% — больший.
Медиана, как уже отмечалось, делит упорядоченный вариационный ряд на две равные но численности группы.
Наряду с медианой можно рассматривать величины, называемые квантилями, которые делят ряд распределения на 4 равные части, на 10 и т. д.
Квантили, которые делят ряд на 4 равные по объему совокупности, называются квартилями. Различают нижний Q1/4 и верхний Q3/4 квартили (рис. 6). Величина Q1/2 является медианой. Вычисление квартилей совершенно аналогично вычислению медианы:
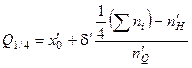 ; (3)
; (3)
 , (4)
, (4)
где x0 — минимальная граница интервала, содержащего нижний (верхний) квартиль; nH — частота (относительная частота), накопленная до квартального интервала; nQ — частота (относительная частота) квартильного интервала; d — величина квартального интервала.
Процентили делят множество наблюдений на 100 частей с равным числом наблюдений в каждой. Децили делят множество наблюдений на десять равных частей. Квантили легко вычисляются по распределению накопленных частот (по кумуляте).
Мода. Модой в статистике называется наиболее часто встречающееся значение признака, т. е. значение, с которым наиболее вероятно можно встретиться в серии зарегистрированных наблюдений.
В дискретном ряду мода (Мо)—это значение с наибольшей частотой.
В интервальном ряду (с равными интервалами) модальным является класс с наибольшим числом наблюдений. Значение моды находится в его пределах и вычисляется по формуле

где x0 — нижняя граница модального интервала; d — величина интервала; 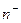 — частота интервала, предшествующего модальному; nMo — частота модального класса;
— частота интервала, предшествующего модальному; nMo — частота модального класса;  — частота интервала, следующего за модальным.
— частота интервала, следующего за модальным.
В совокупностях, в которых может быть произведена лишь операция классификации объектов по какому-нибудь качественному признаку, вычисление моды является единственным способом указать некий центр тяжести совокупности.
К недостаткам моды следует отнести следующие: невозможность совершать над ней алгебраические действия; зависимость ее величины от интервала группировки, возможность существования в ряду распределения нескольких модальных значений признака (см., например, рис. 4, в).
Сравнение средних. Целесообразность использования того или иного типа средней величины зависит по крайней мере от следующих условий: цели усреднения, вида распределения, уровня измерения признака, вычислительных соображений. Цель усреднения связана с содержательной трактовкой рассматриваемой задачи. Однако форма распределения может существенно усложнить исследование средних. Если для симметричного распределения (см. рис. 4, а) мода, медиана и среднее арифметическое тождественны, то для асимметричного распределения это не так. На выбор средней может повлиять и вид распределения. Например, для ряда с открытыми конечными интервалами нельзя вычислять среднее арифметическое, но если распределение близко к симметричному, можно подсчитать тождественную ему в этом случае, медиану.
Показатели колеблемости (вариации) значений признаков. Для характеристики рядов распределения оказывается недостаточным указание только средней величины данного признака, поскольку два ряда могут иметь, к примеру, одинаковые средние арифметические, но степень концентрации (или, наоборот, разброса) значений признаков вокруг средней будет совершенно различной. Характеристикой такого разброса служат показатели колеблемости — разность между- максимальным и минимальным значениями признака в некоторой совокупности (вариационный размах), а также другие показатели: среднее абсолютное (линейное) отклонение, среднее квадратическое отклонение и т. п.
Дисперсия. Дисперсией называется величина, равная среднему значению квадрата отклонений отдельных значений признаков от средней арифметической. Обозначается дисперсия s2 и вычисляется по формуле
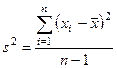 (6)
(6)
Корень квадратный из дисперсии называется средним квадратическим отклонением и обозначается.
Геометрически среднее квадратическое отклонение является показателем того, несколько в среднем кривая распределения размыта относительно ее среднего арифметического. Измеряется в тех же единицах, что и изучаемый признак.
При ручном счете для упрощения вычислений дисперсию (s) рассчитывают по формуле методом отсчета от условного нуля. Для интервального ряда с равными интервалами процедура следующая. Сначала вычисляются центры интервалов. Относительно какого-либо отобранного серединного интервала ряда, например А, вверх и вниз выписывается натуральный ряд чисел (аi) соответственно со знаком «плюс» и «минус»: 0, +1, +2 и т. д.; -1,
-2 и т. д. (табл. 4).
Далее вычисляются величины  . В качестве промежуточного результата по формуле (7) получаем среднее арифметическое. Величина дисперсии получается подстановкой промежуточных величин из табл. 4 в формулу (8).
. В качестве промежуточного результата по формуле (7) получаем среднее арифметическое. Величина дисперсии получается подстановкой промежуточных величин из табл. 4 в формулу (8).
Среднее арифметическое находится по формуле[87]
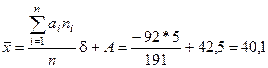 (лет) (7)
(лет) (7)
Тогда дисперсия равна
 (8)
(8)
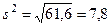 (лет)
(лет)
Приведенные вычисления показывают, что при среднем возрасте 40 лет все остальные члены совокупности имеют возраст, который в среднем отклоняется от 40 лет на 7,8 лет, т. е. примерно на 20%.
Таблица 4 . Пример вычисления дисперсии*
| Центр возрастной группы xi | Частота или относительная частота ni или mi | 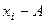
| 
| 
| 
| 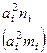
|
| 27,5 32,5 37,5 А = 42,5 | -15 -10 -5 | -3 -2 -1 | -45 -74 -52 | |||
| 47,5 52,5 57,5 | ||||||
| d = 5 | 
| 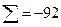
| 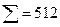
|
* Численные данные о распределении кандидатов наук по возрастным группам в отделении экономики, истории, философии и права АН УССР (Организация науки/ Под ред. Г. М. Доброва, М., 1970, с. 148—149).
Среднее абсолютное отклонение. Эта мера вариации представляет собой среднее арифметическое из абсолютных величин отклонений отдельных значений признака от их среднего арифметического
 (9)
(9)
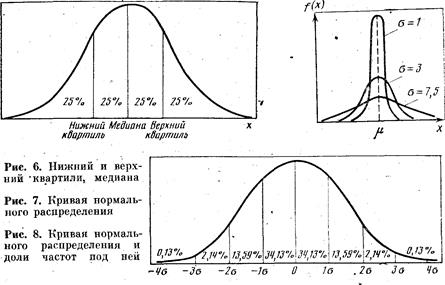
где  означает, что суммируются значения отклонений без учета знака этих отклонений;
означает, что суммируются значения отклонений без учета знака этих отклонений;  — объем совокупности.
— объем совокупности.
.Вместо среднего арифметического в формуле 9 часто берут моду или медиану. Для симметричных распределений мода, медиана и среднее арифметическое совпадают и выбор средней не представляет труда. Для асимметричного распределения иногда отдают предпочтение медиане.
Величина среднего квадратического отклонения всегда больше d и для достаточно большой выборочной совокупности с распределением признака, близкого к нормальному, связана с  соотношением
соотношением

Например, для данных табл. 4 вреднее линейное отклонение, подсчитанное по формуле 9, равно d = 6,3 года. Тогда
s = 1,25*6,3 = 7,87
что с учетом погрешности вычислений совпадаете найденным ранее средним квадратическим отклонением. Таким образом, для предварительного анализа можно заменить вычисление менее трудоемким вычислением.
Коэффициент вариации. Среднее линейное и среднее квадратическое отклонение являются мерой абсолютной колеблемости признака и всегда выражаются в тех же единицах измерения, в которых выражен изучаемый признак. Это не позволяет сопоставлять между собой средние отклонения различных признаков (в случае разных единиц измерения) в одной и той же совокупности, а также одного и того же признака в разных совокупностях с различными средними. Чтобы иметь такую возможность, средние отклонения часто выражаются через соотнесение в процентах к среднему арифметическому, т.е. в виде относительных величий.
Отношение среднего линейного или среднего квадратического отклонения к среднему арифметическому называется коэффициентом вариации (V):
 (11)
(11)
 (12)
(12)
Очевидно, что тот из рядов имеет большее рассеяние, у которого коэффициент вариации больше.
Рассмотренные выше показатели вариации применимы лишь к количественным признакам, а точнее к признакам, измеренным не ниже чем по интервальной шкале. Применение этих мер для низших уровней, строго говоря, некорректно и требует тщательной интерпретации полученных результатов.
Вариации качественных признаков. Если признак имеет k взаимоисключающих градаций, то для вычисления индекса качественной вариации применяется - процедура, поясняемая .следующим примером.
Пусть получено следующее распределение ответов (взаимоисключающих) на вопросы А, В и С (колонка 1):
| A | ||
| B | ||
| C | ||
Во вторую колонку запишем такие частоты, которые получились бы при равномерном заполнении всех трех вопросов, т. е. 120/3 = 40. Теперь вычислим величину
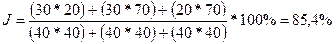 (13)
(13)
Этот показатель называется индексом качественной вариации и указывает на степень неоднородности полученных ответов. Если бы все ответы попали лишь в одну градацию, то J=0, что означало бы полное единство в ответах, хотя, конечно, индекс совершенно не учитывает того, в какую именно градацию попали все эти ответы.
Совершенно аналогично индекс вычисляется при любом числе градаций. Но для альтернативных признаков вариация обычно подсчитывается по формуле (14). Она отличается от J на константу, называется дисперсией, выражается в абсолютных числах и обозначается s2:
 (14)
(14)
Другой мерой вариации признака (независимо от уровня измерения) может служить так называемая энтропия — мера неопределенности, вычисляемая по формуле
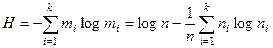 . (15)
. (15)
Логарифм в этой формуле может быть взят по любому основанию. Энтропия обладает следующими свойствами:
а) энтропия равна нулю лишь в том случае, если вероятность получения одного из значения xi, признака x равна единице (вероятность остальных значений при этом равна нулю). Такой признак не обладает неопределенностью, так как достоверно известно одно единственно возможное его значение. Во всех остальных случаях, когда имеется та или иная неопределенность в значениях xi, энтропия является положительной величиной;
б) наибольшей энтропией обладает признак, когда все, значения xi равновероятны. Для признака с k градациями

Отсюда видно, что максимальная энтропия увеличивается с ростом числа градаций в признаке,
5. Нормальное распределение. Статистические гипотезы
Адекватное применение количественных методов, вошедших в практику социологических исследований, в той или иной степени опирается на предположение, что изучаемый признак (или совокупность признаков) подчиняется определенному статистическому закону распределения. Таким наиболее часто встречающимся распределением является нормальный закон, представление о котором дано здесь в очень кратной форме.
Вторая группа вопросов, рассмотренных в этом разделе, связана с проверкой гипотез. Можно выделить две функции статистических процедур: во-первых, это описание элементов совокупности, во-вторых, помощь исследователю в принятии некоторых решений о них. В предыдущих разделах этой главы их рассмотрение было связано с дескриптивной функцией статистики. Здесь же кратко описаны основные понятия и принципы статистического вывода.
Нормальное распределение. Наиболее широко известным теоретическим распределением является нормальное, или гауссовское, распределение. Нормальное распределение признака наблюдается в тех случаях, когда на величину его значений действует множество случайных независимых или слабозависимых факторов, каждый из которых играет в общей сумме примерно одинаковую и малую роль (т. е. отсутствуют доминирующие факторы), Функция плотности гауссовского распределения имеет вид

где 2 — дисперсия случайной величины (2 — это теоретическая дисперсия, отличающаяся от s2, вычисляемой по выборочным данным); m — среднее значение (математическое ожидание) (рис. 7).
В практических расчетах часто используется так называемое правило трех сигм, которое заключается том, что лишь 0,26% всех значений нормально распределенного признака лежат вне интервала m±3, т. е. почти все значения признака укладываются в интервалеиз шести сигм (рис. 8).
Статистические гипотезы. Статистической называют гипотезу о виде неизвестного распределения либо о параметрах известных распределений[88]. Так, статистической будет гипотеза о том, что переменная в генеральной совокупности распределена по нормальному закону. Проверяемую гипотезу называют нулевой (основной) гипотезой и обозначают Но. Наряду с нулевой рассматривается конкурирующая гипотеза /Л (альтернативная), которая ей противоречит.
Статистический критерий и проверка гипотез. Для проверки нулевой гипотезы используется специально подобранная случайная величина, точное, либо приближенное распределение которой известно и обычно сведено в таблицы. Эта величина называется статистическим критерием. Обозначим его пока К.
Для критерия К фиксируется так называемая критическая область, т. е. совокупность значений критерия, при которых нулевую гипотезу отвергают. Точка Kкр называется критической, если она отделяет критическую область от области принятия гипотезы.
Различают правостороннюю, левостороннюю и двустороннюю критические области.
Принятие или отверженце гипотезы производится на основе соответствующего статистического- критерия с определенной вероятностью. Считают, что пулевая гипотеза справедлива, если вероятность того, что критерий К примет значение, большее Kкр, т. е. попадет в критическую область, равна выбранному значению вероятности a, т. е.
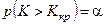 (для правосторонней области);
(для правосторонней области);
 (для левосторонней области);
(для левосторонней области);
 (для двусторонней области).
(для двусторонней области).
Принятая вероятность a называется уровнем значимости.
Практически принятие или отвержение нулевой гипотезы проводится следующим образом: выбирается соответствующий критерий (этот вопрос будет обсуждаться далее); вычисляется наблюдаемое значение критерия KH, исходя из эмпирического распределения; выбирается уровень статистической значимости (обычно 0,05 или 0,01).
По таблице распределения критерия К для данного уровня значимости находят критическую точку Kкр. Если KH>Kкр, нулевую гипотезу отвергают, если же KH<Kкр, то ее отвергать нет основания.
Делая такие выводы (т. е. принимая или отвергая гипотезу), можно совершить ошибки двух типов: отвергнуть гипотезу, когда она верна; принять ее, когда она неверна. Поэтому при принятии гипотезы было бы неверным считать, что она тем самым полностью доказана. Для большей уверенности необходимо ее проверять другими способами (например, увеличить объем выборки).
Отвергают гипотезу более категорично, чем принимают.
Примеры статистических гипотез: а) нормальное распределение имеет заданное среднее и дисперсию либо имеет заданное среднее (о дисперсии ничего не говорится); б) распределение нормальное либо два неизвестных распределения одинаковы.
В качестве критериев чаще всего используются случайные величины, распределенные нормально (2—критерий), по закону Фишера (F — критерий Фишера), по закону Стьюдента (критерий Стьюдента), по закону хи-квадрат (критерий c2) и т. д.
В качестве конкретного примера рассмотрим применение критерия хи-квадрат для проверки гипотезы о виде распределения изучаемого признака.
Критерий хи-квадрат. Популярность критерия хи-квадрат обусловлена главным образом тем, что применение его не требует предварительного знания закона распределения изучаемого признака. Кроме того, признак может принимать как непрерывные, так и дискретные значения,, причем измеренные хотя бы на поминальном уровне.
Если закон распределения признака неизвестен, по есть основания предположить, что он имеет определенный вид А, то критерий c2 позволяет проверить гипотезу: исследуемая совокупность распределена по закону А. Для проверки такой гипотезы сравниваются эмпирические (наблюдаемые) и теоретические (вычисленные в предположении определенного распределения А) частоты. Выпишем эти частоты:
| Значения признака | x1 | x2 | ..., | xk |
| Эмпирические частоты | n1 | n2 | ..., | nk |
| Теоретические частоты | 
| 
| ..., | 
|
Как правило, эмпирические и теоретические частоты будут различаться. Возможно, что наблюдаемое различие случайно (статистически незначимо) и объясняется либо малым числом наблюдений, либо способом их группировки, либо иными причинами. Но возможно, что расхождение частот значимо и объясняется тем, что теоретические частоты вычислены исходя из неверной гипотезы о характере распределения значений рассматриваемых признаков, генеральной совокупности. Критерий c2 отвечает на вопрос, случайно или нет такое расхождение частот. Как любой критерий, c2 не доказывает справедливость гипотезы, а лишь с определенной вероятностью а устанавливает ее согласие или несогласие с данными наблюдениями.
Критерий c2 имеет вид
 (17)
(17)
Критическая точка распределения c2 находится; (см. табл. Б приложения) по заданному уровню значимости a, и числу степеней свободы df. Число степеней свободы находят по формуле
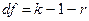 ,
,
где k — число интервалов вариационного ряда; r — число параметров предполагаемого распределения, которые оценены по данным выборки (например, для нормального распределения оценивают двапараметра: m и s2).
Рассмотрим пример, когда признак оценивался в терминах очень низкий, средний), очень высокий и был получен следующий ряд распределения для этих трех категорий:
| Очень низкий | Средний | Очень высокий | |

|
Проверим гипотезу о том, что в генеральной совокупности значения этого признака распределены равномерно.
Теоретическое распределение для этих групп получим,если предположим, что эти категории независимы, т. е. респондент с одинаковой вероятностью может попасть в любую группу. Очевидно, ожидаемая (теоретическая) частота будет равна 24/3 = 8 человек.
Таким образом, имеем следующие эмпирические и теоретические частоты:
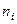
| |||
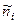
|
Проверяется гипотеза, что число респондентов во всех трех категориях одинаково, т. е. отличие распределения от равномерного статистически незначимо.
Вычислим величину  по формуле (17):
по формуле (17):

По таблице распределения c2, например, для уровня значимости 0,05 и степени свободы, равном df = 3 – 1 = 2, находим критическую точку  . Таким образом, наблюдаемое значение c2 меньше
. Таким образом, наблюдаемое значение c2 меньше  , следовательно, данные наблюдений согласуются с нулевой гипотезой и не дают оснований ее отвергнуть.
, следовательно, данные наблюдений согласуются с нулевой гипотезой и не дают оснований ее отвергнуть.
Хи-квадрат-критерий применим и для проверки нулевой гипотезы об отсутствии связей между признаками в случае, если эмпирические данные сгруппированы не по одному, как выше, а по нескольким признакам. Например, пусть имеется выборка в 190 человек, чье мнение относительно какого-то определенного вопроса исследовалось (табл. 5). Расчленим эту выборку па три независимых категории по возрасту. Рассмотрим следующие гипотезы: Н0 — не существует различия мнений относительно этого вопроса среди различных возрастных групп; Н1 — существует различие. Проверим гипотезу для уровня значимости a = 0,05.
Таблица 5.Пример для вычисления c2
| Ответ | Возраст опрашиваемого | Всего | ||
| более 40 | 25-40 | менее 25 | ||
| Категорически не согласен Не согласен Согласен Полностью согласен Всего | (а)18 (г)23 (а)11 (л)8 | (б)13 (д)13 (и)14 (м)16 | (в)10 (ж)12 (к)23 (н)29 |
Для нахождения ожидаемой (теоретической) частоты в любой плетке таблицы необходимо просто перемножить соответствующие маргинальные частоты и разделить произведение на итоговую сумму. Например, ожидаемая частота для клетки (а) равна

Процедуру вычисления представим в табл. 6. Число степеней свободы определяется по формуле
Дата добавления: 2015-09-29; просмотров: 861;
