СХЕМА 3 5 страница
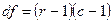
где r — число строк, а с — число столбцов в табл. 5.
Для нашего примера df = (4—1)(3—1) == 6. По табл. Б приложения находим, что c2 = 16,812. Следовательно, нужно отвергнуть гипотезу о том, что нет различий в мнении среди неодинаковых возрастных групп, т. е. можно предположить, что существует значимая статистическая взаимосвязь между тем, к какой возрастной группе принадлежит респондент, и тем мнением, которое он высказывает. Однако величина c2 не говорит о силе связи между переменными, а лишь указывает на вероятность существования такой связи. Для определения интенсивности связи необходимо использовать соответствующие меры связи.
Для корректного применения методов, основанных на c2, исследователь должен обеспечить выполнение следующих условий. Выборку необходимо получить из независимых наблюдений. Данные могут быть измерены на любом уровне, по ни одна из ожидаемых частот не должна быть слишком мала (минимум 5). Если же частоты оказываются менее 5, то необходимо либо уменьшить степень дробности группировки признаков, объединив соседние категории, либо обратиться к другому критерию[89].
Таблица 6.Схема вычисления c2
| Ячейка (табл. 5) | Частота 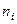
| Ожидаемая частота 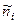
| 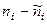
| 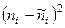
| 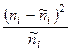
|
| а б в г д ж з и к л м н | 12,9 12,1 16,0 15,2 14,1 18,7 15,2 14,1 18,7 16,7 15,6 20,6 | 5,1 0,9 6,0 7,8 1,1 6,7 4,2 0,1 4,3 8,7 0,4 8,4 | 26,01 0,81 36,00 60,84 1,21 44,89 17,64 0,01 18,49 75,69 0,16 70,56 | 2,016 0,067 2,250 4,003 0,086 2,400 1,160 0,001 0,989 4,532 0,010 3,425 | |

|
6. Статистические взаимосвязи и их анализ
Понятие о статистической зависимости. Исходя из известного положения исторического материализма о всеобщей взаимозависимости и взаимообусловленности явлений общественной жизни, социолог-марксист не может ограничиться изучением отдельно взятого явления изолированно от других процессов и событий, а должен стремиться по возможности охватить весь комплекс явлений, относящихся к тому или иному социальному процессу и изучить существующие между ними зависимости.
Различают два вида зависимостей: функциональные (примером которых могут служить законы Ньютона в классической физике) и статистические.
Закономерности массовых общественных явлений складываются под влиянием множества причин, которые действуют одновременно и взаимосвязанно. Изучение такого рода закономерностей в статистике и называется задачей о статистической зависимости. В этой задаче полезно различать два аспекта: изучение взаимозависимости между несколькими величинами и изучение зависимости одной или большего числа величин от остальных. В основном первый -аспект связан с теорией корреляций (корреляционный анализ), второй — с теорией регрессии (регрессионный анализ). Основное внимание в этом параграфе уделено изучению взаимозависимостей нескольких признаков, а основные принципы регрессионного анализа рассмотрены очень кратко.
В основе регрессионного анализа статистической зависимости ряда признаков лежит представление о форме, направлении и тесноте (плотности) взаимосвязи.
В табл. 7 приведено эмпирическое распределение заработной платы рабочих в зависимости от общего стажа работы (условные данные) для выборки в 25 человек,
Таблица 7. Распределение заработной платы и общего стажа работы
| Номер респондента | Общий стаж работы ( 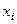 ), лет ), лет
| Заработная плата  , руб. , руб.
| 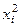
| 
| 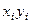
|
| n = 25 | 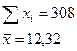
| 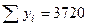

| 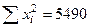
| 
| 
|
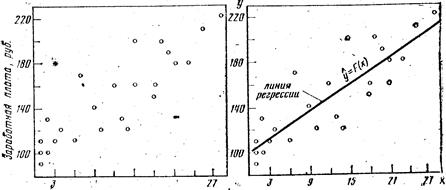
а на рис. 9 эти численные данные представлены в виде так называемой диаграммы рассеяния, или разброса. Вообще говоря, визуально не всегда можно определить, существует или нет значимая взаимосвязь между рассматриваемыми признаками и насколько она значима, хотя очень часто уже на диаграмме просматривается общая тенденция в, изменении значений признаков и направление связи между изучаемыми признаками.
Уравнение регрессии. Статистическая зависимость одного или большего числа признаков от остальных выражается о помощью уравнений регрессии. Рассмотрим две величины х и y, такие, например, как на рис. 9. Зафиксируем какое-либо значение переменной х, тогда у принимает целый ряд значений. Обозначим  среднюю величину этих значений у при данном фиксированном х. Уравнение, описывающее зависимость средней величины
среднюю величину этих значений у при данном фиксированном х. Уравнение, описывающее зависимость средней величины 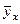 от х, называется уравнением регрессии у по х:
от х, называется уравнением регрессии у по х:
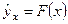
Аналогичным образом можно дать геометрическую интерпретацию регрессионному уравнению[90]
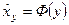
Уравнение регрессии описывает числовое соотношение между величинами, выраженное в виде тенденции к возрастанию (или убыванию) одной переменной величины при возрастании (убывании) другой. Эта тенденция проявляется на основе некоторого числа наблюдений, когда из общей массы выделяются, контролируются, измеряются главные, решающие факторы.
Характер связи взаимодействующих признаков отражается в ее форме. В этом отношении полезно различать линейную и нелинейную, регрессии. На рис. 10, 11 приведены графики линейной и криволинейной форм линий регрессии и их диаграммы разброса для случая двух переменных величии.
Направление и плотность (теснота),линейной связи между двумя переменными измеряются с помощью коэффициента корреляции.
Меры взаимозависимости для интервального уровня измерения.Наиболее широко известной мерой связи служит коэффициент корреляций Пирсона (или, как его иногда называют, коэффициент корреляции, равный произведению моментов). Одно из важнейших предположений, на котором покоится использование коэффициента r, состоит в том, что регрессионные уравнения для изучаемых переменных имеют линейную форму[91], т. е.
 (18)
(18)
либо
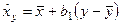 (19)
(19)
где  — среднее арифметическое для переменной у;
— среднее арифметическое для переменной у;  — среднее арифметическое для переменной х;
— среднее арифметическое для переменной х; 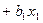
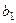 и
и 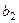 — некоторые коэффициенты.
— некоторые коэффициенты.
Поскольку вычисление коэффициента корреляции и коэффициентов регрессии 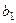 и
и 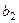 проводится по схожим формулам, то, вычисляя r, получаем сразу же и приближенные
проводится по схожим формулам, то, вычисляя r, получаем сразу же и приближенные
|
|
|
Рис. 9 Диаграмма рассеяния для распределения заработной платы и общего стажа работы
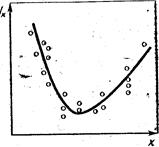
Рис. 10. Линии регрессии для распределения заработной платы и общего стажа работы
х — стаж работы, лет; у — заработная плата, руб.
Рис. 11. Линия регрессии криволинейной формы и диаграмма рассеяния
регрессионные модели[92].
Выборочные коэффициенты регрессии и корреляции вычисляются по формулам
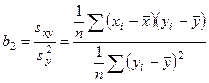 ; (20)
; (20)
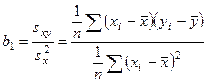 ; (21)
; (21)
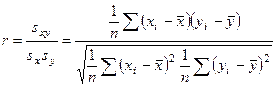 . (22)
. (22)
Здесь 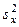 — дисперсия признака х;
— дисперсия признака х; 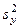 — дисперсия признака у. Величина
— дисперсия признака у. Величина  называется ковариацией x и y.
называется ковариацией x и y.
Расчет r для несгруппированных данных. Для вычислительных целей эти выражения в случае несгруппированных данных можно переписать в следующем виде:

Рассчитаем коэффициент корреляций и коэффициенты регрессии для данных табл. 7:

тогда уравнение регрессии имеет вид
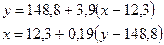
Линии регрессии 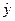 = F(х) изображены на рис. 10. Отсюда видно, что между заработной платой и общим стажем работы существует прямая зависимость: по мере увеличения общего стажа работы на предприятии растет и заработная плата. Величина коэффициента корреляции довольно большая и свидетельствует о положительной связи между переменными величинами. Следует отметить, что вопрос о том, какую переменную в данном случае принимать в качестве зависимой величины, а какую — в качестве независимой, исследователь решает на основе качественного анализа и профессионального опыта. Коэффициент корреляции по определению является симметричным показателем связи:
= F(х) изображены на рис. 10. Отсюда видно, что между заработной платой и общим стажем работы существует прямая зависимость: по мере увеличения общего стажа работы на предприятии растет и заработная плата. Величина коэффициента корреляции довольно большая и свидетельствует о положительной связи между переменными величинами. Следует отметить, что вопрос о том, какую переменную в данном случае принимать в качестве зависимой величины, а какую — в качестве независимой, исследователь решает на основе качественного анализа и профессионального опыта. Коэффициент корреляции по определению является симметричным показателем связи: 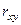 =
= 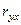 . Область возможного изменения коэффициента корреляции r лежит в пределах от +1 до —1.
. Область возможного изменения коэффициента корреляции r лежит в пределах от +1 до —1.
Вычисление r для сгруппированных данных. Для сгруппированных данных примем ширину интервала по каждой переменной за единицу (если по какой-либо переменной имеются неодинаковые размеры интервала, то возьмем из них наименьший). Выберем также начало координат для каждой переменной где-нибудь возле среднего значения, оцененного на глаз.
Для условных данных, помещенных в табл. 8, за нулевую точку отсчета выберем значение у, равное 64, а по х — значение 134,5.
Тогда коэффициент корреляции определяется по следующей формуле:
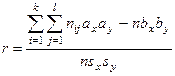
где  — отклонение от условной средней по признаку х;
— отклонение от условной средней по признаку х; 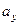 — отклонение от условной средней по признаку у;
— отклонение от условной средней по признаку у; 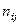 — частота наблюдений по клеткам таблицы;
— частота наблюдений по клеткам таблицы;
Таблица 8.Вычисление r по сгруппированным данным
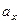
| x | y | Промежуточные результаты | |||||
| -1 | +1 | +2 | 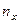
| 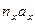
| 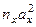
| |||
| +2 +1 -1 -2 | 146,5 140,5 134,5 128,5 122,5 | -41 -32 | ||||||
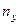

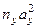
| -26 |
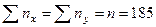
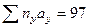
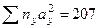
|

|
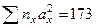
|
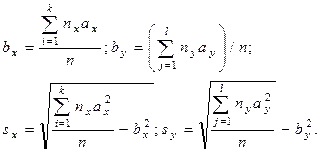
Для вышеприведенного примера порядок вычислений представлен в табл. 9. Для определения 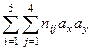 вычислим последовательно все произведения частоты в каждой клетке таблицы на ее координаты. Так
вычислим последовательно все произведения частоты в каждой клетке таблицы на ее координаты. Так
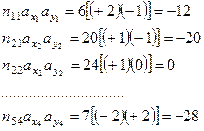
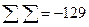
Подсчитаем 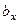 и
и  :
: 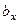 = -17/185 = -0,09;
= -17/185 = -0,09;  = 97/185 = 0,52. Определяем
= 97/185 = 0,52. Определяем  и
и 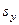 :
:
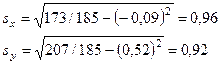
В соответствии с формулой вычисляем

Таким образом, величина связи достаточно велика, как, впрочем, и следовало ожидать на основе визуального анализа таблицы.
Статистическая значимость r. После вычисления коэффициента корреляции возникает вопрос, насколько показателен этот коэффициент и не обусловлена ли зависимость, которую он фиксирует, случайными отклонениями. Иначе говоря, необходимо проверить гипотезу о том, что полученное значение r значимо отличается от 0.
Если гипотеза 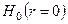 будет отвергнута, говорят, что величина коэффициента корреляции статистически значима (т. е. эта величина не обусловлена случайностью) при уровне значимости a.
будет отвергнута, говорят, что величина коэффициента корреляции статистически значима (т. е. эта величина не обусловлена случайностью) при уровне значимости a.
Для случая, когда n<50, применяется критерий вычисляемый по формуле
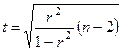
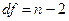 (23)
(23)
Распределение t дано в табл. В приложения.
Если n>50, то необходимо использовать Z-критерий
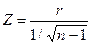
В табл. А приложения приведены значения величины 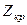 для соответствующих a.
для соответствующих a.
Вычислим величину Z для коэффициента корреляции по табл. 7 (вычисление проделаем лишь для иллюстрации, так как число наблюдений n = 25 и нужно применять критерий t). Величина r (см. табл. 7) равна 0,86. Тогда

Для уровня значимости a = 0,01 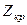 = 2,33 (см. табл. А приложения).
= 2,33 (см. табл. А приложения).
Поскольку Z> 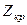 , мы должны констатировать, что коэффициент корреляции r = 0,86 значим и лишь в 1% случаев может оказаться равным нулю. Аналогичный результат дает и проверка по критерию t для a = 0,01 (односторонняя область);
, мы должны констатировать, что коэффициент корреляции r = 0,86 значим и лишь в 1% случаев может оказаться равным нулю. Аналогичный результат дает и проверка по критерию t для a = 0,01 (односторонняя область); 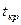 = 2,509, t выборочное равно 8,08.
= 2,509, t выборочное равно 8,08.
Другой часто встречающейся задачей является проверка равенства на значимом уровне двух коэффициентов корреляции 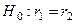 при заданном уровне a, т. е. различия между r1 и r2 обусловлены лишь колебаниями выборочной совокупности.
при заданном уровне a, т. е. различия между r1 и r2 обусловлены лишь колебаниями выборочной совокупности.
Критерий для проверки значимости следующий:
 , (25)
, (25)
где значения 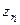 и
и 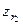 находят по табл. Д приложения для
находят по табл. Д приложения для  и
и  .
.
Значения 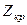 определяют по табл. А приложения аналогично вышеприведенному примеру.
определяют по табл. А приложения аналогично вышеприведенному примеру.
Частная и множественная регрессия и корреляция. Ранее нами было показано, как можно по опытным данным найти зависимость одной переменной от другой, а именно как построить уравнение регрессии вида у = а + bх. Если исследователь, изучает влияние нескольких переменных 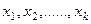 на результатирующий признак у, то возникает необходимость в умении строить регрессионное уравнение более общего вида, т. е.
на результатирующий признак у, то возникает необходимость в умении строить регрессионное уравнение более общего вида, т. е.
 , (26)
, (26)
где а, 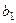 ,
, 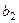 , …….,
, ……., 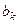 — постоянные коэффициенты, коэффициенты регрессии.
— постоянные коэффициенты, коэффициенты регрессии.
В связи с уравнением (26) необходимо рассмотреть следующие вопросы: а) как по эмпирическим данным вычислить коэффициенты регрессии а, 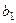 ,
, 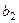 , …….,
, ……., 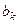 ; б) какую интерпретацию можно приписать этим коэффициентам; в) оценить тесноту связи между у и каждым из
; б) какую интерпретацию можно приписать этим коэффициентам; в) оценить тесноту связи между у и каждым из 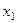 в отдельности (при элиминировании действия остальных); г) оценить тесноту связи между у и всеми переменными
в отдельности (при элиминировании действия остальных); г) оценить тесноту связи между у и всеми переменными 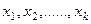 в совокупности.
в совокупности.
Рассмотрим этот вопрос на примере построения двухфакторного регрессионного уравнения. Предположим, что изучается зависимость недельного бюджета свободного времени (у) от уровня образования ( 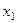 ) и возраста (
) и возраста ( 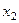 ) определенной группы трудящихся по данным выборочного обследования. Будем искать эту зависимость в виде линейного уравнения следующего вида:
) определенной группы трудящихся по данным выборочного обследования. Будем искать эту зависимость в виде линейного уравнения следующего вида:
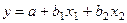
При расчете коэффициентов уравнения множественной регрессии полезно преобразовать исходные эмпирические данные следующим образом. Пусть в результате обследования n человек получены эмпирические значения, сведенные в следующую таблицу (в каждом столбце представлены несгруипированные данные):
| Номер респондента . . . n Среднее по столбцу Среднее квадратическое отклонение | y
y1
y2
.
.
.
yn
 sy
sy
| x1
x11
x12
.
.
.
x1n
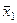 s1
s1
| x2
x21
x22
.
.
.
x2n
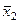 s2
s2
|
Каждое значение переменной в таблице преобразуем по формулам
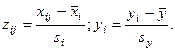
Это преобразование называется нормированием переменных. В результате искомое регрессионное уравнение примет вид
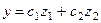
Коэффициенты 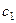 и
и 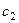 находятся по следующим формулам:
находятся по следующим формулам:
 (27)
(27)
 (28)
(28)
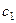 и
и 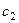 называются стандартизированными коэффициентами регрессии. Следовательно, зная коэффициенты корреляции между изучаемыми признаками, можно подсчитать коэффициенты регрессии. Подставим конкретные значения
называются стандартизированными коэффициентами регрессии. Следовательно, зная коэффициенты корреляции между изучаемыми признаками, можно подсчитать коэффициенты регрессии. Подставим конкретные значения  из следующей таблицы[93]:
из следующей таблицы[93]:
| y x1 x2 Среднее Среднее квадратическое отклонение | y 31,6 16,5 | x1 0,556 9,0 2,9 | x2 -0,131 -0,027 30,2 11,5 |
Тогда
 .
.
Аналогично 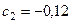 , и уравнение регрессии запишется в виде
, и уравнение регрессии запишется в виде 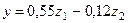 .
.
Коэффициенты исходного регрессионного уравнения 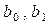 и
и  находятся по формулам
находятся по формулам
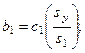 (29)
(29)
 (30)
(30)
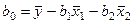
Подставляя сюда данные из вышеприведенной таблицы, получим 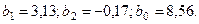
Как же следует интерпретировать это уравнение? Например, значение  показывает, что в среднем недельный бюджет свободного времени при увеличении возраста на один год и при фиксированном признаке
показывает, что в среднем недельный бюджет свободного времени при увеличении возраста на один год и при фиксированном признаке 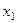 , уменьшается на 0,17 час. Аналогично интерпретируется
, уменьшается на 0,17 час. Аналогично интерпретируется 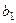 . (Исходные эмпирические данные можно изобразить на диаграмме рассеяния аналогично тому, как это сделано на рис. 10, но уже в трехмерном пространстве (
. (Исходные эмпирические данные можно изобразить на диаграмме рассеяния аналогично тому, как это сделано на рис. 10, но уже в трехмерном пространстве (  ,
, 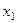 ,
, 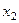 ))
))
Коэффициенты 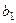 ,
,  можно в то же время рассматривать и как показатели тесноты связи между переменными у и, например,
можно в то же время рассматривать и как показатели тесноты связи между переменными у и, например, 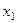 при постоянстве
при постоянстве 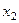 .
.
Аналогичную интерпретацию можно применять и к стандартизированным коэффициентам регрессии 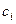 . Однако поскольку
. Однако поскольку 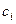 вычисляются исходя из нормированных переменных, они являются безразмерными и позволяют сравнивать тесноту связи между переменными, измеряемыми в различных единицах. Например, в вышеприведенном примере
вычисляются исходя из нормированных переменных, они являются безразмерными и позволяют сравнивать тесноту связи между переменными, измеряемыми в различных единицах. Например, в вышеприведенном примере 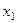 измеряется в классах, а
измеряется в классах, а 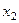 — в годах
— в годах 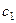 и
и 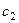 позволяют сравнить, насколько
позволяют сравнить, насколько 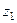 теснее связан с у, чем
теснее связан с у, чем 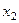 [94].
[94].
Поскольку коэффициенты 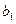 и
и 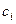 измеряют частную одностороннюю связь, возникает необходимость иметь показатель, характеризующий связь в обоих направлениях. Таким показателем является частный коэффициент корреляции
измеряют частную одностороннюю связь, возникает необходимость иметь показатель, характеризующий связь в обоих направлениях. Таким показателем является частный коэффициент корреляции
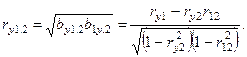
Для рассматриваемого примера 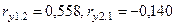 . Для любых трех переменных
. Для любых трех переменных 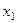 ,
, 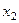 ,
, 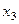 частный коэффициент корреляции между двумя из них при элиминировании третьей строится следующим образом,
частный коэффициент корреляции между двумя из них при элиминировании третьей строится следующим образом,
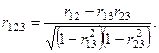 (31)
(31)
Аналогично можно определить и частные коэффициенты корреляции для большего числа переменных (  ). Однако ввиду громоздкости вычисления они применяются достаточно редко.
). Однако ввиду громоздкости вычисления они применяются достаточно редко.
Для характеристики степени связи результатирующего признака у с совокупностью независимых переменных служит множественный коэффициент корреляции 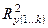 , который вычисляется по формуле (иногда он выражается в процентах)
, который вычисляется по формуле (иногда он выражается в процентах)
Дата добавления: 2015-09-29; просмотров: 706;
