Насколько Вы лично удовлетворены следующими сторонами своей жизни? 2 страница
Кроме того, необходимо учитывать следующие критерии:
а) каждая категория (суждение) должна обладать минимальной ошибкой;
б) ошибки должны иметь случайный характер. Если же какая-то одна частная ошибка встречается значительно чаще, чем другая, то это значит, что признак не принадлежит шкальному типу. Суждение, которое не удовлетворяет этим требованиям, отбрасывается.
В более сложных шкалах вместо ответов да, нет респондентам можно предложить оценить каждое суждение, например, по шкале: 4 — полностью согласен; 3 — согласен; 2 — не знаю, не могу ответить; 1 — не согласен; 0 — категорически не согласен.
Процедура построения шкалограммы в этом случае совершенно аналогична дихотомическому случаю. Баллы при ранжировании вопросов и ответов равны сумме отмеченных значений отдельных вопросов. Коэффициенты репродуктивности для таких шкал могут быть повышены как за счет выбрасывания отдельных вопросов, не укладывающихся в шкалограмму, так и путем укрупнения числа градаций ответов на вопрос (например, ответы с пятью градациями укрупнить до трех градаций: 2 — согласен; 1 — не знаю; 0 — не согласен).
Построенная шкала предъявляется обследуемой совокупности респондентов, причем все суждения шкалы предварительно тасуются в беспорядке. Ранг опрашиваемого определяется по сумме набранных баллов.
Подсчитав средний ранг для различных групп респондентов, можно проранжировать сами группы относительно измеряемого свойства.
Основное преимущество шкалограммного анализа состоит в однозначности балла, получаемого респондентом в отличие от ранее рассмотренных методов шкалирования.
К недостаткам шкалы относятся большие технические и ряд теоретических трудностей, связанных с ее построением. Кроме того, одномерность не является инвариантной чертой шкалы, т. е. данная шкала может быть одномерной для одной группы индивидов и не быть таковой для другой.
Семантический дифференциал. Метод семантического дифференциала (СД) разработан Ч. Осгудом для измерения смысла понятий и слов и прежде всего для дифференциации эмоциональной стороны значения данного понятия[140]. В социологии и
|
психологии метод СД чаще всего применяется при изучении эмоциональных компонентов социальных установок.
Для определения отношения респондентов к сопоставляемым между собой объектам (словам) используется следующая процедура. Допустим, требуется измерить различие установок к числу детей в семье. Измерение производится по набору шкал, каждая из которых представляет собой континуум, образованный парой антонимичных прилагательных. Континуум содержит семь градаций интенсивности отношения. Например, по шкале хорошее — плохое оценка объекта устанавливается следующим образом: очень хорошее (+3), хорошее (+2), немного хорошее (+1), ни хорошее, ни плохое (0), немного плохое (—1), плохое (—2), очень плохое (—3). Каждый респондент выражает свое отношение к числу детей в семье по всему набору шкал, число которых зависит от целей исследования и ограничивается объемом опросного листа. Критерием отбора шкал является частота употребления антонимов в языке и способность шкалы вызывать реакции по всему пространству континуума при оценке самых различных слов.
После заполнения опросного листа оценки каждого из респондентов по каждой шкале суммируются, затем вычисляется средняя арифметическая оценка объекта установки для группы в целом. Если полученные средние нанести на график, составленный из вычерченных в масштабе шкал измерения, и соединить таким образом найденные точки ломаной линией, то можно получит профиль данного объекта. На рис., 13 наглядно представлены различия репродуктивных установок при опросе группы из 107 человек[141].
Различие в отношении к числу детей в семье графически выражается расстояниями между средними оценками сопоставляемых объектов по каждой шкале. Однако это различие установок точнее может быть выражено посредством вычисления величины дифференциала Д. Расчет осуществляется по формуле
где Д — величина дифференциала, показывающая степень различия в отношении к объектам х и у по набору из п шкал; d — разность средних оценок объектов х и у по шкале i. Величина дифференциала выражается положительным числом, и чем ближе оно к нулю, тем выше сходство в отношении к сопоставляемым объектам. Данные табл. 29 показывают различие установок к числу детей (расчет произведен по 15 шкалам, 9 из которых представлены на рис. 13).
Таблица 29
| Объекты оценки (число детей) | ||||
| — 2,72 5,46 7,62 | 2,72 — 3,97 6,49 | 5,46 3,97 — 2,62 | 7,62 6,49 2,62 — |
Сопоставление абсолютных значений дифференциалов позволяет сделать вывод о том, что различия репродуктивных установок весьма существенны и что установки объединяются в две самостоятельные группы: установки на малодетность (Д12) и установки на среднедетность (Д34), так как величины Д12 и Д34 меньше величины Д23 — соответственно 2,72 — 2,62 — 3,97.
Следует отметить, что Ч. Осгуд и его коллеги при разработке методики СД и ее применении в различных областях познания выявили общую меру, на основе которой выносятся человеческие оценки. Она состоит из трех критериев или факторов, которые в совокупности определяют эмоциональный аспект значения исследуемого понятия.
Каждый из трех факторов, а именно оценки, силы и активности, представлен набором тесно связанных между собой шкал, отражающих отдельные аспекты человеческого восприятия показания органов чувств. Наиболее употребительными для фактора оценки являются: хорошее — плохое, светлое — темное, чистое — грязное; для факторов силы: сильное — слабое, тяжелое — легкое, твердое — мягкое; для фактора активности: активное — пассивное, быстрое — медленное, теплое — холодное. Обычно, определяя набор шкал (эта задача является главной при использовании метода СД), исходят из специфики оцениваемых объектов в стремятся к тому, чтобы представить все три основных фактора, (имеются также и другие факторы, но они встречаются редко и их применение обусловлено специальными целями исследования).
Многие исследователи считают, что в принципе методика СД позволяет фиксировать только оценочную сторону отношения, и поэтому часто прибегают к вычислению дифференциала не по шкалам каждого из основных факторов в отдельности, а в целом по -всему набору применяющихся шкал. Надо сказать, что рассмотрение названных факторов как трех координат измерения значения, как трех осей семантического пространства встречается в основном в психолингвистике, а также при описании истории создания методики СД и практически в социологии используется крайне редко.
Метод СД достаточно сложен и трудоемок, тем не менее его применение оправдывается возможностями выявления различий в реакциях на вербальные объекты.
3. Надежность измерения социальных характеристик
Описанные выше способы построения шкал не дают полного представления о свойствах полученных оценок. Для этого необходимы дополнительные процедуры, результаты которых будем описывать в терминах ошибок измерения. Назовем это проблемой надежности измерения. Рассмотрим ее решение на пути выявления правильности измерения, его устойчивости и обоснованности.
Компоненты надежного измерения. При изучении правильности устанавливается общая приемлемость данного способа измерения. Непосредственно понятие правильности связано с возможностью учета в результате измерения различного рода систематических ошибок. Систематические ошибки имеют некоторую стабильную природу возникновения: либо они являются постоянными, либо меняются по определенному закону.
Устойчивость характеризует степень совпадения результатов измерения при повторных применениях, измерительной процедуры и описывается величиной случайной ошибки. Наиболее сложный вопрос надежности измерения — его обоснованность. Обоснованность связана с доказательством того, что измерено вполне определенное заданное свойство объекта, а не некоторое другое, более или менее на него похожее.
При установлении надежности следует иметь в виду, что в процессе измерения участвуют три составляющие: объект измерения, измеряющие средства, с помощью которых производится отображение свойств объекта на числовую систему, и субъект, производящий измерение. Предпосылки надежного измерения кроются в каждой отдельной составляющей.
Прежде всего сам объект в отношении измеряемого свойства может обладать значительной степенью неопределенности. Так, зачастую у индивида нет четкой иерархии жизненных ценностей, а следовательно, нельзя получить и абсолютно точные данные, характеризующие важность для него тех или иных явлений.
Но может быть и так, что способ получения оценки не обеспечивает максимально точных значений измеряемого свойства. Например, у респондента существует определенная иерархия ценностей, а для получения информации используется поминальная оценка с вариациями ответов от очень важно до совсем неважно. Как правило, из приведенного набора все ценности помечаются стартами очень важно, важно, хотя реально у респондента имеется большее число уровней значимости.
Наконец, при наличии высокой точности первых двух составляющих измерения субъект, производящий измерение, допускает грубые ошибки. Например, в процессе клинического интервью, в ходе которого должна быть выявлена система ценностей опрашиваемого, интервьюер не смог довести до респондента суть беседы не смог добиться доброжелательного отношения к исследованию и пр.
Каждая составляющая процесса измерения может быть источником ошибки, связанной либо с устойчивостью, либо с правильностью, либо с обоснованностью. Однако, как правило, исследователь не в состоянии разделить эти ошибки по источникам их происхождения и поэтому изучает ошибки устойчивости, правильности и обоснованности всего измерительного комплекса в совокупности. При этом правильность (как отсутствие систематических ошибок) и устойчивость информации — элементарные предпосылки надежности. Наличие существенной ошибки в этом отношении уже сводит на нет проверку данных измерения на обоснованность.
В, отличие от правильности и устойчивости, которые могут быть измерены достаточно строго и выражены в форме числового показателя, критерии обоснованности определяются либо на основе логических рассуждений, либо на основе косвенных показателей. В смежных с социологией науках, например в психологии, проблема обоснованности теста решается путем сопоставления его результатов с результатами внешнего критерия — с известной группой или с данными реального поведения. В социологии такой прием, как правило, не удается использовать, поэтому обычно применяется сравнение данных одной методики с данными других методик или исследований, т. е. обоснованность устанавливается более косвенным путем. При этом, разумеется, не обязательно добиваться полного соответствия результатов. Достаточным будет установление общих тенденций, что зависит и от соотносительной значимости самих критериев, и от их функции в общем замысле исследования.
Правильность измерения — выявление систематических ошибок.Прежде чем приступать к изучению таких компонентов надежности, как устойчивость и обоснованность, необходимо убедиться в правильности выбранного инструмента измерения (шкалы или системы шкал).
Возможно, что последующие этапы окажутся излишними, если в самом начале выяснится полная неспособность данного инструмента на требуемом уровне дифференцировать изучаемую совокупность, или может оказаться, что систематически не используется какая-то часть шкалы или ее отдельная градация. Прежде всего нужно ликвидировать или уменьшить такого рода недостатки шкалы и только затем использовать ее в исследовании.
Отсутствие разброса ответов по значениям шкалы. Попадание ответов в один пункт свидетельствует о полной непригодности измерительного инструмента —шкалы. Такая ситуация может возникнуть или из-за нормативного давления в сторону общепринятого мнения, или из-за того, что градации (значения) шкалы п имеют отношения к определению данного свойства у рассматриваемых объектов (нерелевантны).
Например, если все опрашиваемые респонденты согласны с утверждением хорошо, когда работа или задание требуют универсальных знаний, нет ни одного ответа не согласен, остается только зафиксировать этот факт, однако подобная шкала не поможет дифференцировать изучаемую совокупность по отношению респондентов к работе.
Часто примером нерелевантности являются многие исходные шкалы методики семантического дифференциала Осгуда. Так, в частности, при изучении установок инженера в работе измерения респондентов по шкалам мужской — женский, горячий — холодный и др. давали оценку только в середине шкалы, в нейтральной точке. Уточнение позволило сделать вывод, что эти шкалы, по мнению респондентов, не имеют отношения к изучаемым установкам.
Использование части шкалы. Довольно часто обнаруживается, что практически работает лишь какая-то часть шкалы, какой-то один из ее полюсов с прилегающей более или менее обширной зоной.
Так, если респондентам для оценки предлагается шкала, имеющая положительный и отрицательный полюса, в частности от +3 до —3, то при оценивании какой-то заведомо положительной ситуации респонденты не используют отрицательные оценки, а дифференцируют свое мнение лишь с помощью положительных. Для того чтобы вычислить значение относительной ошибки измерения, исследователь должен знать определенно, какой же метрикой пользуется респондент — всеми семью градациями шкалы или только четырьмя положительными. Так, ошибка измерения в 1 балл мало о чем говорит, если мы не знаем, какова действительная вариация мнений.
Пример[142]. Девятнадцати испытуемым было предложено высказать отношение к трем понятиям по семи шкалам к каждому. Шкалы имели по 21 градации с крайними полюсами +10 и —10 и средней точкой 0. В целом получено 399 (19*3*7) оценок со следующим распределением:
Балл (  )
| -1 | … | -3-4 | … | -6-7 | … | -10 | |||||||||||
Частота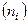 
|
Поскольку значения <0 использовались всего, лишь 11 раз (3+3+5) из 399, т. е. в 2,8% случаев, то возникает вопрос, действует ли отрицательная часть этой шкалы. Возможно, что попадание в эту часть шкалы — явление чисто случайное. Проверим предположение.
Будем считать, что если вероятность р попадания в конец шкалы не превышает 5% при достаточно малом уровне значимости (a = 0,05 или a. = 0,01), то наблюдаемые попадания ответов являются случайными и соответствующая часть шкалы не работает. Для этого границы доверительного интервала, построенного по имеющейся частоте для вероятности попадания в конец шкалы, сравним со значением 5 %. Если значение 5 % оказывается выше границ этого интервала, то следует признать, что проверяемая часть шкалы «не работает».
Для расчета границ доверительного интервала воспользуемся формулами[143]
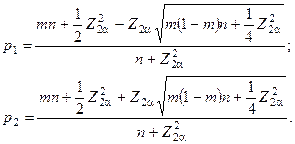(1)
Здесь m — доля попаданий в проверяемую часть шкалы; п — объем выборочной совокупности данных; Z — коэффициент доверия, соответствующий 2a (о доверительном оценивании см. с. 211).
Для рассматриваемого примера т — 0,0276; п — 399;Za = 1,96 для a = 0,05. Подставляя эти значения в формулы, получим р1 = 0,016, р2 = 0,049. То же самое в процентах: р1 = 1,6%; р2 = 4,9%. Постольку значение 5% не принадлежит интервалу (1,6%; 4,9%), то считаем, что отрицательная часть шкалы ( <0) не работает, следовательно, 21-балльная оценка функционирует лишь в области от +10 до 0.
Для вопросов, имеющих качественные градации ответов, можно применять подобное требование в. отношении каждого пункта шкалы: каждый из них должен набирать не менее 5% ответов, в противном случае считаем этот пункт шкалы неработающим.
Требование 5%-го уровня наполнения в двух рассмотренных задачах не следует рассматривать как строго обязательное в зависимости от задач исследования могут быть выдвинуты большие или меньшие значения этих уровней.
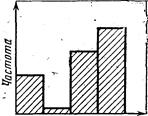
Неравномерное использование отдельных пунктов шкалы. Случается, особенно при использовании упорядоченных шкал, .градации которых сопровождаются словесными описаниями, что некоторое значение переменной (признака) систематически выпадает из поля зрения респондентов, хотя соседние градации, характеризующие более низкую и более высокую степень выраженности признака, имеют существенное наполнение.
Так, если конфигурация распределения ответов на вопрос с четырьмя упорядоченными градациями такая, как на рис. 14, то, видимо, шкала неудачно сформулирована. Значительное наполнение
|
двух соседних пунктов (1 и 3) свидетельствует о захвате части голосов из плохо сформулированного пункта 2.
|
— четырем, пять — трем и т. д. При этом базовые оценки
используются значительно чаще, чем другие.
Для выявления указанных аномалий равномерного распределения по шкале можно предложить следующее правило: для достаточно большой доверительной вероятности (1—a³ 0,99) и, следовательно, в достаточно широких границах наполнение каждого значения не должно существенно отличаться от среднего из соседних наполнений.
Соответствующий статистический критерий таков;
Эта величина имеет хи-квадрат распределение с одной степенью свободы (df = 1).
Здесь i — номер значения признака, который подвергается анализу; 
— наблюдаемая частота для этого значения;
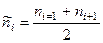- ожидаемая частота, как средняя из двух соседних.
Пример. Рассмотрим случай измерения в десятибалльной шкале ряда ценностей типа любимая работа, материальный достаток, здоровье и т. д. При 45 испытуемых и 14 предложенных ценностях получены 623 оценки, распределение которых выглядит так
|
| ||||||||||
|
|
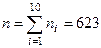
Поскольку предполагается, что шкала должна работать равномерно, то, возможно, пункты шкалы 9, 7, 5 не удовлетворяют этому требованию.
Для оценки = 9 наблюдаемая частота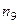 
= 67, ожидаемая —
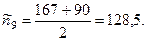
Подставим данные значения в формулу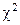 
и получим расчетную величину 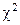= 22,93. Поскольку 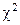= 22,93> 
= 6,63 (a = 0,01), то следует признать различие между наблюдаемой и ожидаемой частотами значимым. Следовательно, частота 67 для оценки a = 9 слишком мала по сравнению с соседними.
Аналогичные расчеты проводятся для пунктов шкалы a = 7 и a = 5; частота пункта 7 ( = 60) не противоречит выдвинутому требованию равномерности; частота оценки 5 ( 
= 81) слишком велика по сравнению с соседними и, таким образом, противоречит требованию равномерности.
Определение грубых ошибок. В процессе измерения иногда возникают грубые ошибки, причиной которых могут быть неправильные записи исходных данных, плохие расчеты, неквалифицированное использование измерительных средств и т. п. Это проявляется в том, что в рядах измерений попадаются данные, резко отличающиеся от совокупности всех остальных значений. Чтобы выяснить, нужно ли эти значения признать грубыми ошибками, устанавливают критическую границу так, чтобы вероятность превышения ее крайними значениями была достаточно малой и соответствовала некоторому уровню значимости а. Это правило основано на том, что появление в выборке чрезмерно больших значений хотя и возможно как следствие естественной вариабельности значений, но маловероятно.
Если окажется, что какие-то крайние значения совокупности принадлежат ей с очень малой вероятностью, то такие значения признаются грубыми ошибками и исключаются из дальнейшего рассмотрения. Выявление грубых ошибок особенно важно проводить для выборок малых объемов: не будучи исключенными из анализа, они существенно искажают параметры выборки.
Статистический критерий т определения грубых ошибок таков (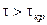 
, где в качестве 
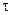выступает либо 
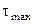, либо 
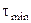)[144]
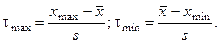(2)
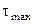Здесь и 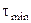являются крайними членами некоторой совокупности значений {х}.
В табл. XII, приводимой В. Ю. Урбахом[145], даны критические значения 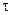, соответствующие различным объемам выборки для доверительных уровней: a = 0,05 и a = 0,01.
Например, при выборке в 50 единиц значение 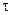для уровня a = 0,05 будет 3,16.
Если 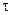расчетное окажется больше 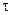критического, то соответствующее х считается маловероятным и отбрасывается как грубая ошибка.
Пример. Представим, что получены распределения по признаку с такими выборочными параметрами: 
= 0,012; s = 0,160 (при объеме выборки п = 29 респондентов). В этом распределении крайними значениями оказались такие: 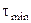= —0,500; 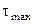= 0,250. Существенное подозрение вызывает значение, равное —0,500, поскольку среднее значение этого признака близко к 0 (0,012), а вариация его значений невелика (s = 0,160).
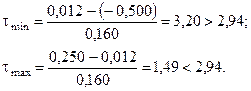
Так как для п = 29 и a = 0,05 
= 2,94, то с вероятностью 0,95 можно признать, что значение признака х = —0,500 слишком мало для данной совокупности и поэтому является грубой ошибкой, а х = 0,250 не относится к резко выделяющимся значениям.
Итак, дифференцирующая способность шкалы как первая существенная характеристика ее надежности предполагает: обеспечение достаточного разброса данных, выявление фактического использования респондентом предложенной протяженности шкалы; анализ отдельных выпадающих значений, исключение грубых ошибок. После того как установлена относительная приемлемость используемых шкал в указанных аспектах, следует переходить к выявлению устойчивости измерения .по этой шкале.
Устойчивость измерения. О высокой надежности шкалы можно говорить лишь в том случае, если повторные измерения при ее помощи одних и тех же объектов дают сходные результаты: Устойчивость проверяется на одной и той же выборке исследуемых объектов (респондентов). Сравнение же средних оценок разных выборок ничего не говорит об устойчивости измерения как таковом, а только лишь о репрезентативности выборок и их соответствии одной и той же совокупности. Обычно устойчивость проверяют проведением двух последовательных замеров с определенным временным интервалом — таким, чтобы этот промежуток не был слишком велик, чтобы сказалось изменение самого объекта, но не слишком мал, чтобы респондент мог по памяти подтягивать данные второго замера к предыдущему (т. е. его протяженность зависит от объекта изучения и колеблется от двух до трех недель).
Осуществление более двух измерений связано с трудностями организации эксперимента и накапливанием ошибок другой природы, не связанной с устойчивостью.
Пусть x — изучаемый на устойчивость признак, отдельные его значения —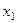 
, 
, 
, …, 
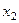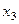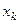. Каждый респондент l (l = 1, ..., n)и при первом и при второе опросах получает некоторую оценку по изучаемому признаку — 
и 
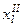соответственно.
Результаты двух опросов п респондентов заносятся в таблицу сопряженности (табл. 30), которая служит основой для дальнейшего изучения вопросов устойчивости.
Здесь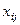 
— число респондентов, выбравших в первом опросе ответ 
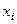и заменивших его при втором опросе на ответ 
.
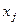Существует традиция изучать устойчивость с помощью анализа корреляций между ответами проб I и II. Однако этот подход недостаточно эффективен, поскольку не учитывает многих аспектов устойчивости.
Таблица 30
| Опрос I | Опрос II |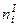 
| ||
| …
| …
| …
| ||
|
.
.
.
.
.
.
|  …
.
.
.
.
.
.
| 
.
.
.
.
.
.
| 
.
.
.
.
.
.
| 
.
.
.
.
.
.
|
|  …
|  …
|  …
|  …
|
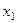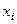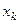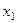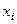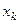
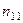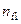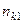
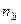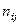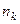
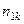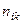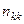
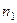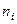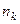
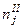
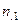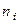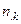Дата добавления: 2015-09-29; просмотров: 640;