Насколько Вы лично удовлетворены следующими сторонами своей жизни? 3 страница
Остановимся на более результативных показателях.
1. Показателем абсолютной устойчивости шкалы назовем величину, показывающую долю совпадающих ответов в последовательных пробах
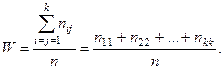 (3)
(3)
Этот показатель использует не всю информацию, содержащуюся в соотношении ответов проб I и II, а базируется лишь на частотах совпадающих ответов. Однако он хорош, например, для характеристики устойчивости качественных признаков.
Для описания устойчивости количественных признаков его недостаточно, поскольку при большом числе градаций доля совпадающих ответов будет чрезвычайно мала и значение W мало информативно. Здесь пригодны показатели неустойчивости, т. е. величины ошибки, учитывающие не просто факт несовпадения ответов, а степень этого несовпадения. Ошибки рассчитываются по крайней мере для порядковых признаков.
Линейной мерой несовпадения оценок является средняя арифметическая ошибка, показывающая средний сдвиг в ответах в расчете на одну пару последовательных наблюдений:
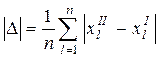 (4)
(4)
Здесь  и
и 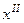 — ответы по анализируемому вопросу l-то респондента в I и II пробах соответственно.
— ответы по анализируемому вопросу l-то респондента в I и II пробах соответственно.
Пример. Пусть ответы на вопрос в пятибалльной шкале для выборки 50 человек распределились, как в табл. 31.
Таким образом, в I пробе оценку «1» дали 9 респондентов, из них только трое повторили ее в пробе II, пятеро отметили «2», один дол оценку «3» и т. д.
Таблица 31. Распределение ответов в двух пробах
| Проба I | Проба II | Сумма | ||||
| — — — | — | — | — — | |||
| å |
Ошибка такого соотношения ответов:
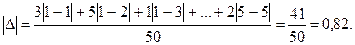
Данный показатель использует всю информацию, содержащуюся в распределении, хорошо интерпретируется как средний сдвиг в ответах одного респондента, однако имеет определенные ограничения аналитического характера и поэтому обычно редко используется в статистических расчетах.
Средняя квадратическая ошибка для последовательных данных[146] в расчете на одну пару наблюдений выглядит так:
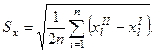 (5)
(5)
Для данных табл. 31 эта ошибка будет равна
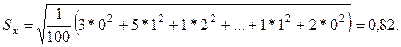
(совпадение 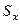 и
и 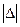 в этом примере чисто случайное).
в этом примере чисто случайное).
До сих пор речь шла об абсолютных ошибках, размер которых выражался в тех же единицах, что и сама измеряемая величина, например 0,82 балла в пятибалльной шкале. Это не позволяет сравнивать ошибки измерения разных признаков по разным шкалам. Следовательно, помимо абсолютных, нужны относительные показатели ошибок измерения.
В качестве показателя для нормирования абсолютной ошибки можно использовать максимально возможную ошибку в рассматриваемой шкале ( 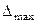 ).
).
Если число делений шкалы k, тогда 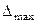 равно разнице между крайними значениями шкалы (
равно разнице между крайними значениями шкалы ( 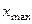 —
— 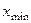 ), т. е. k —1, и относительная ошибка имеет вид
), т. е. k —1, и относительная ошибка имеет вид
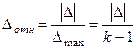
(здесь 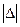 — средняя арифметическая ошибка измерения).
— средняя арифметическая ошибка измерения).
Однако зачастую этот показатель плохо работает из-за того, что шкала не используется на всей ее протяженности. Поэтому более показательными являются относительные ошибки, рассчитанные по фактически используемой части шкалы, как было рассмотрено выше. Если число градаций в; работающей части шкалы обозначить  , то тогда более надежной будет такая оценка ошибки:
, то тогда более надежной будет такая оценка ошибки:

Если в качестве абсолютной ошибки использовалась средняя квадратическая ошибка S, то показатель относительной ошибки
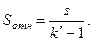
Пример. Допустим, что шкала имеет 7 градаций. При определении «работающей» части этой шкалы анализируется распределение полученных в I пробе оценок:
| Оценка | ||||||||
| Частота | 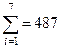
|
Здесь на оценки 5, 6, 7 приходится лишь 11 наблюдений, т. е. 2,26%. Проверка согласно критерию (формула (1)) устанавливает, что эта часть шкалы не работает, т. е. используются лишь градации 1, 2, 3, 4, поэтому 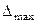 = 4 — 1 = 3. На основании соотношения ответов в I и II пробах находим сдвиги в ответах (ошибки). Распределение ошибок по этой шкале оказалось следующим:
= 4 — 1 = 3. На основании соотношения ответов в I и II пробах находим сдвиги в ответах (ошибки). Распределение ошибок по этой шкале оказалось следующим:
| Значение ошибки | —4 | —3 | —2 | —1 | |||||
| Частота | 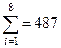
|
Таким образом, 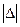 = 0,60 и относительная ошибка
= 0,60 и относительная ошибка 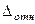 =
= 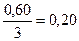 , или 20%, и
, или 20%, и 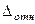 =
= 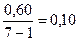 — явно завышенная точность измерения. Однако оценка по
— явно завышенная точность измерения. Однако оценка по  также является довольно грубой и не использует, всю информацию, содержащуюся в ответах I пробы, ведь реально не все оценки могут дать максимальный сдвиг, а только крайние на шкале.
также является довольно грубой и не использует, всю информацию, содержащуюся в ответах I пробы, ведь реально не все оценки могут дать максимальный сдвиг, а только крайние на шкале.
Оценим для приведенного распределения максимальный сдвиг по реально работающей части шкалы: только крайние значения (233,78+11) могут дать сдвиг в 3 балла, 106 и 59 ответов могут дать максимальный сдвиг в 2 балла. Таким образом, возможный сдвиг для данного исходного распределения может быть равен средней в 2,6 балла четырехбалльной шкалы, т. е. фактическая ошибка еще больше: 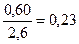 .
.
Повышение устойчивости измерения. Для решения этой задачи необходимо выяснить различительные возможности пунктов используемой шкалы, что предполагает четкую фиксацию респондентами отдельных значений: каждая оценка должна быть строго отделена от соседней. На практике это означает, что в последовательных пробах респонденты практически повторяют свои оценки. Следовательно, высокой различимости делений шкалы должна соответствовать малая ошибка.
Эту же задачу можно описать в терминах чувствительности шкалы, которая характеризуется количеством делений, приходящихся на одну и ту же разность в значениях измеряемой величины, т. е. чем больше градаций в шкале, тем больше ее чувствительность. Однако чувствительность нельзя повышать простым увеличением дробности, ибо высокая чувствительность при низкой устойчивости является излишней (например, шкала в 100 баллов, а ошибка измерения ±10 баллов).
Но и при малом числе градаций, т. е. при низкой чувствительности, может быть низкая устойчивость, и тогда следует увеличить дробность шкалы. Так бывает, когда респонденту навязывают категорические ответы да, нет, а он предпочел бы менее жесткие оценки. И потому он выбирает в повторных испытаниях иногда да, иногда нет для характеристики своего нейтрального положения.
Итак, следует найти некоторое оптимальное соотношение между чувствительностью и устойчивостью. Введем правило: использовать столько градаций в шкале, чтобы ее ошибка была меньше 0,5 балла.
Если ошибка меньше -0,5 балла, то в последовательных опросах ответы в среднем будут совпадать. При 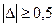 балла ответы в последовательных опросах будут в среднем отличаться на 1 балл (и выше).
балла ответы в последовательных опросах будут в среднем отличаться на 1 балл (и выше).
Существуют способы, позволяющие добиться требуемой чувствительности.
Пример. В исследовании каждый испытуемый дает 8 оценок некоторым профессиональным качествам инженеров. Значение оценок варьирует от +3 до —3. Проведено два измерения. Рассмотрим суммарное распределение оценок по четырем качествам (самостоятельность, творчество, инициативность, опытность), данных тринадцати респондентов (табл. 32).
Всего в табл. 32 представлено 416 пар наблюдений: 13 респондентов ×8 оценок ×4 качества. Из них в первой пробе 226 оценок имели значение 3; во второй пробе из них только 170 были повторены, 47 оценок получили значение 2, 6 оценок — значение I и 3 оценки — значение 0.
Таблица 32.Распределение ответов в двух пробах
Проба 
| Проба 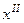
| 
| 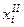
| 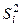
| 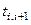
| ||||||
| —1 | —2 | —3 | |||||||||
| —1 —2 —3 | 2,70 2,47 2,18 1,06 2,67 0,25 —1,50 | 0,3383 0,4547 1,3962 1,8175 0,2044 0,6875 0,2500 | 3,01 1,96 3,39 1,95 | ||||||||
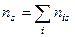
| 2,44 |
Таким образом, дли исходной оценки 3 средняя оценка во второй пробе стала равной
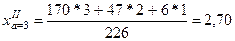 и т.д.
и т.д.
На основании этого соотношения оценок получим распределение ошибок:
| Значения ошибок | —3 | —2 | —1 | ||||||
| Частоты ошибок | å = 416 |
Рассчитаем среднюю арифметическую ошибку 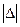 = 0,69.
= 0,69.
Поскольку 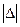 >0,5, ищем неразличающиеся градации.
>0,5, ищем неразличающиеся градации.
Средние оценки по каждой строке сравниваем с помощью критерия Стьюдента. Если окажется, что 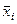 и
и 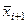 отличаются незначимо (
отличаются незначимо ( 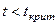 ), то далее нужно сравнивать
), то далее нужно сравнивать 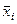 и
и 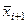 и т. д. до значимого отличия средних (
и т. д. до значимого отличия средних ( 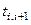 записаны в последнем столбце табл. 32, а значимые значения выделены).
записаны в последнем столбце табл. 32, а значимые значения выделены).
|
|
| |
Здесь все оценки попадают в три непересекающихся класса: оценка 3 отличается от 2; 2 и I не отличаются друг от друга, но отличаются от соседних оценок; последние четыре значения взаимно неразличимы.
Следовательно, респонденты различают лишь три уровня вместо семи предложенных, и шкала должна быть преобразована в трехбалльную, где высокой оценке соответствует исходная оценка в 3 балла, средней — 2 и 1 балл; низкой — 0, —1, —2, —3. Присвоим описанным уровням новые баллы — соответственно 3, 2, 1. В итоге имеем следующее соотношение оценок (табл. 33).
Это распределение характеризуется ошибкой 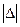 = 0,43 балла, т. е. уже меньше 0,5 градации, и потому такая шкала устойчива.
= 0,43 балла, т. е. уже меньше 0,5 градации, и потому такая шкала устойчива.
Таблица 33.Итоговое распределение оценок
| Проба I | Проба II | å | ||
| å |
В общем случае возможны два варианта соотношения исходных оценок: 1) классы неразличимости оценок не пересекаются (на пример, как это было в только что рассмотренном случае):
| |
|
|
2) классы неразличимости оценок пересекаются, например, так
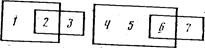
В первом случае можно подобрать для шкалы числовую серию, т. е. упорядоченный ряд чисел, в котором большее число характеризует более высокий уровень качества.
Во втором случае имеется полуупорядоченная система оценок, и ее можно отобразить лишь на полуупорядоченную числовую систему. В рассматриваемом примере возможно, в частности, такое числовое представление:
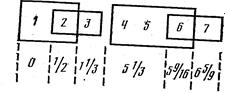
Там, где между исходными оценками нет существенного различия, разница между значениями числового представления (нижний ряд чисел) меньше 1; при значимом различии разница больше 1.
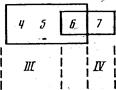
Однако часто желательно иметь преобразованные оценки, выраженные целыми числами. В таком случае можно предложить следующую систему понижения дробности шкалы: ближайшим исходным значениям, существенно отличающимся друг от друга, присваивают ранги последовательно I, II, III и т. д. В рассматриваемом, примере это будет выглядеть так:
|
Для промежуточных значений, несущественно отличающихся от соседних (например, исходную оценку 2 можно отнести в любые классы — и в I, и во -II), следует предложить дополнительные критерии отнесения их в один из двух соседних классов. Можно в качестве критерия использовать меру относительной близости промежуточной оценки к тому или иному соседнему классу и путем перебора всех возможных схем объединения искать схему с наименьшей ошибкой.
В конечном итоге порядок действия может быть таким. На основе данных двух последовательных проб определяем пороги различаемости градаций шкалы. В том случае, если обнаружено смешение градаций, применяют один из двух способов.
Первый способ. В итоговом варианте уменьшают дробность шкалы (например, из шкалы в 7 интервалов переходят на шкалу в 3 интервала).
Второй способ. Для предъявления респонденту сохраняют прежнюю дробность шкалы и только при обработке укрупняют соответствующие ее пункты (как это было показано выше).
Второй способ кажется предпочтительнее, поскольку, как правило, большая дробность шкалы побуждает респондента и к более активной реакции. При обработке данных информацию следует перекодировать в соответствии с проведенным анализом различительной способности исходной шкалы.
Итак, предложенные способы анализа целесообразны при отработке окончательного варианта методики. Анализ устойчивости отдельных вопросов шкалы позволяет: а) выявить плохо сформулированные вопросы, их неадекватное понимание разными респондентами; б) уточнить интерпретацию шкалы, предложенной для оценки того или иного явления, выявить более оптимальный вариант дробности значения шкалы.
Изучение устойчивости окончательного варианта методики даст представление о надежности данных (связанной с устойчивостью), которые будут получены в основном исследовании. 1
Обоснованность измерения. Проверка обоснованности шкалы предпринимается лишь после того, как установлены достаточные правильность и устойчивость измерения исходных данных. Как уже отмечалось, проверка обоснованности — достаточно сложный процесс и, как правило, не до конца разрешимый, И поэтому нецелесообразно сначала применять трудоемкую технику для выявления обоснованности, а после этого убеждаться в неприемлемости данных вследствие их низкой устойчивости.
Обоснованность данных измерения — это доказательство соответствия между тем, что измерено, и тем, что должно было быть измерено. Некоторые исследователи предпочитают исходить из так называемой наличной обоснованности, т. е. обоснованности в понятиях использованной процедуры. Например, считают, что удовлетворенность работой — это то свойство, которое содержится в ответах на вопрос: Удовлетворены ли Вы работой? В серьезном социологическом исследовании, имеющем целью проверку некоторых теоретических гипотез, такой сугубо эмпирический подход неприемлем.
Остановимся на возможных формальных подходах к выяснению уровня обоснованности методики. Их можно разделить на три группы: 1) конструирование типологии в соответствии с целями исследования на базе нескольких признаков; 2) использование параллельных данных; 3) судейские процедуры.
Первый вариант нельзя считать формальным методом — это всего лишь некоторая схематизация логических рассуждений, начало процедуры обоснования, которая может быть на этом закончена, а может быть подкреплена более мощными средствами.
Второй вариант требует использования по крайней мере двух источников для выявления одного и того же свойства. Обоснованность определяется степенью согласованности соответствующих данных.
В последнем случае мы полагаемся на компетентность судей, которым предлагается определить, измеряем лимы нужное нам свойство или что-то иное.
Рассмотрим предложенные варианты последовательно.
Конструированная типология. Один из способов — использование контрольных вопросов, которые в совокупности с основными дают большее приближение к содержанию изучаемого свойства, раскрывая различные его стороны.
Например, можно определять удовлетворенность работой лобовым вопросом: Устраивает ли Вас Ваша нынешняя работа? Комбинация его с двумя другими косвенными: Хотите ли Вы перейти на другую работу? и Предположим, что Вы по каким-то причинам временно не работаете. Вернулись бы Вы на свое прежнее место работы? — позволяет произвести более надежную дифференциацию респондентов. Типология по пяти упорядоченным группам от наиболее удовлетворенных работой до наименее удовлетворенных проводится помощью логического квадрата.
Обоснованность в подобного рода типологии не доказывается каким-либо формальным критерием и опирается на логические доводы.
Единственное требование, которое может быть выдвинуто при конструировании такого рода типологии, — это положительная корреляция между составляющими ее признаками. Отсутствие положительной взаимосвязи между вопросами может свидетельствовать, о том, что мы не понимаем сущности измеряемого явления.
Так, попытка построить типологию самостоятельности инженера в работе на базе двух вопросов — сложность получаемых инженером заданий (плюс за сложность) и обращение его за консультациями (плюс за самостоятельное решение) — оказалась неудачной, ибо вопросы коррелировали отрицательным образом и как раз сложность задания предполагала обращение к консультациям.
Параллельные данные. Нередко целесообразно разработать два равноправных приема измерения заданного признака, что позволяет установить обоснованность методов относительно друг друга, т. е. повысить общую обоснованность путем сопоставления двух независимых результатов.
Классифицируем параллельные процедуры в зависимости от соотношения методов и исполнителей: а) несколько методов — один исполнитель; б) один метод — несколько исполнителей; в) несколько методов — несколько исполнителей.
Несколько методов — один исполнитель. Здесь один и тот же исполнитель использует два или более различных метода для измерения одного и того же свойства.
Рассмотрим различные способы использования этого метода, и прежде всего — эквивалентные шкалы. Понятие эквивалентности тесно связано здесь с психологическим явлением социальной установки. Всевозможные акты поведения, обусловленные некоторой установкой, или состояние предрасположенности к определенному поведению составляют целостность (универсум) данной предрасположенности. Универсум можно описать совокупностью признаков.
Возможны равнозначные выборки признаков для описания — измерения социальной установки. Эти выборки и образуют параллельные шкалы, обеспечивая параллельную надежность.
Каждую шкалу рассматриваем как способ измерения некоторого свойства и в зависимости от числа параллельных шкал имеем ряд способов измерения. В качестве исполнителя выступает респондент, дающий ответы одновременно по всем параллельным шкалам. Все ответы сортируем в зависимости от принадлежности к шкале и таким образом получаем параллельные данные.
При обработке такого рода данных следует выяснить два момента: 1) непротиворечивость пунктов отдельной шкалы; 2) согласованность оценок по разным шкалам.
Первая проблема возникает в связи с тем, что модели ответов не представляют идеальной картины: ответы нередко противоречат друг другу. Такая противоречивость свойственна как кумулятивным, так и некумулятивным шкалам. Поэтому встает вопрос, что принимать за истинное значение оценки респондента на данной шкале.
Вторая проблема непосредственно касается сопоставления параллельных данных.
Рассмотрим пример неудавшейся попытки повысить надежность измерения признака удовлетворенность инженера профессией с помощью трех параллельных порядковых шкал. Приведем две из них:
Шкала А
| 11. Профессия мне очень нравится 1. Профессия скорее нравится, чем не нравится 8. Трудно сказать, нравится ли мне моя профессия 14. Эта профессия мне скорее не нравится, чем нравится 3. Профессия мне совершенно не нравится |
Шкала В
| 2. Моя профессия — одна из лучших 13. Считаю, что моя профессия не хуже многих других 5. Моя профессия не хуже в не лучше других 12. Считаю, что есть много профессий, которые лучше моей 4. Моя профессия хуже, чем многие другие |
15 суждений (в порядке, обозначенном слева) предъявляются респонденту общим списком, и он должен выразить свое согласие или несогласие с каждым из них. Каждому суждению присваивается оценка, соответствующая его рангу в указанной шкале (справа). (Например, согласие с суждением 4 дает оценку 1, согласие с суждением 11 —оценку 5 и т. д.).
Рассматриваемый здесь способ предъявления суждений списком дает возможность проанализировать пункты шкалы на непротиворечивость. При использовании упорядоченных номинальных шкал обычно считается, что пункты, образующие шкалу, взаимно исключают друг друга и респондент легко найдет тот из них, который ему подходит.
Изучение распределений ответов доказывает, что респонденты выражают согласие с противоречивыми (с точки зрения исходной гипотезы) суждениями. Например, по шкале 5 42 человека из 100 одновременно согласились с суждениями 13 и 12, т. е, с двумя противоположными суждениями.
Наличие в ответе противоречивых суждений приводит к необходимости вычислять ошибку противоречивости. Это будет разница в рангах, наиболее противоположных для данной шкалы суждений в ответе респондента.
Итак, средние ошибки, характеризующие противоречивость для рассматриваемых шкал, оказались равными
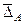 = 0,37;
= 0,37; 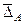 = 1,57.
= 1,57.
Ошибка в 1,57 балла при пятибалльной оценке, видимо, слишком велика, чтобы считать шкалу приемлемой.
Для эквивалентных шкал итоговая оценка респондента рассчитывается как суммарная (или усредненная) оценка по разным шкалам. Однако для правомерности такой процедуры необходимо установить соответствие оценок респондента по всем рассматриваемым шкалам.
В вышеприведенном примере такого соответствия не наблюдалось, что сказалось на коэффициенте корреляции r = —0,02.
Поиск эквивалентной процедуры для повышения надёжности шкалы — весьма утомительная и кропотливая операция. Поэтому данный прием можно рекомендовать лишь при разработке ответственных психологических тестов или методик, предназначенных для массового употребления или панельных исследований.
Один метод — несколько исполнителей. Если метод надежен, то разные исполнители дадут совпадающую информацию, но если их результаты плохо согласуются, то либо измерения ненадежны, либо результаты отдельных исполнителей нельзя считать равноценными. В последнем случае надо установить, нельзя ли считать какую-либо группу результатов заслуживающей большего доверия. Решение этой задачи тем более важно, если предполагается, что одинаково допустимо получение информации любым из рассматриваемых методов (например, использование самооценок против оценок. Анализ параллельных данных с помощью описанных ниже процедур позволит установить правильность такого предположения.
Для количественных признаков при решении вопроса о согласованности оценок нескольких исполнителей предлагается выявить ошибки соответствия одним из приемов, рассмотренных при изучении устойчивости. Прежде всего, поскольку мы имеем здесь случай прямых групповых наблюдений, наиболее адекватной оценкой совпадения данных является средняя квадратическая ошибка.
Пусть каждый раз измерение производят два человека, и респонденту приписывается значение в виде средней (х) из двух исходных. Оценку точности такого измерения следует производить по формуле
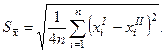 (8)
(8)
Пример. Двое судей оценивают опытность инженера в работе по семибалльной шкале. Предположим, что 13 респондентов получили такие оценки:
| Судья | Респондент | ||||||||||||
| А В | |||||||||||||
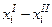
|
Дата добавления: 2015-09-29; просмотров: 807;
