Однородные уравнения
Однородным тригонометрическим уравнением n-й степениотносительно 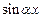 и
и 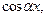
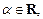 называется уравнение вида
называется уравнение вида
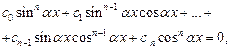 (7.27)
(7.27)
где 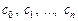 – действительные числа,
– действительные числа, 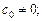
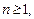
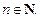
В уравнении (7.27) 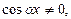 так как при
так как при 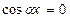 исходное уравнение примет вид:
исходное уравнение примет вид: 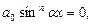 откуда
откуда 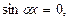 что невозможно, поскольку
что невозможно, поскольку 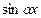 и
и 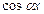 не могут одновременно равняться нулю.
не могут одновременно равняться нулю.
Разделив исходное уравнение на 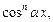 получим:
получим:
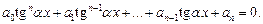
С помощью замены 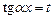 имеем алгебраическое уравнение
имеем алгебраическое уравнение
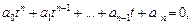
которое решаем и возвращаемся к старой переменной.
Пример 11.Решить уравнение 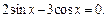
Решение.Разделив уравнение на 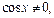 получим
получим 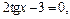 откуда
откуда 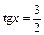 и
и 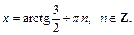
Получаем ответ: 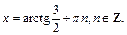
Пример 12. Решить уравнение 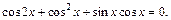
Решение.Используя формулу 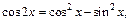 приведем данное уравнение к однородному:
приведем данное уравнение к однородному:
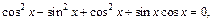
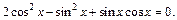
Разделим почленно на 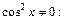
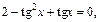
откуда
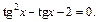
Введем замену 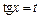 и получим уравнение
и получим уравнение 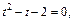 корнями которого будут
корнями которого будут 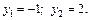
После чего перейдем к решению совокупности простейших уравнений:
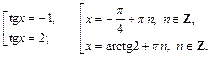
Получаем ответ: 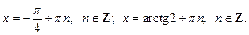
Дата добавления: 2015-09-29; просмотров: 755;
