Уравнения, решаемые с помощью замены переменной
Пример 8.Решить уравнение 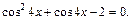
Решение.Данное уравнение является квадратным относительно 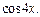 Заменяем
Заменяем 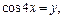 получим уравнение
получим уравнение 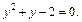 Его корни
Его корни 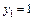 и
и 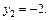 Таким образом, решение исходного уравнения свелось к решению совокупности простейших уравнений:
Таким образом, решение исходного уравнения свелось к решению совокупности простейших уравнений:
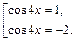
Уравнение 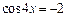 корней не имеет, т. е.
корней не имеет, т. е. 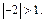
Решением второго является:
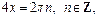
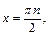
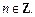
Получаем ответ: 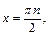
Пример 9.Решить уравнение 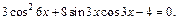
Решение.Используем тождество 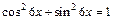 и формулу
и формулу 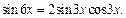 Уравнение сводится к виду
Уравнение сводится к виду
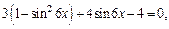
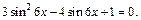
Мы получили квадратное уравнение относительно 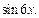 Заменяем
Заменяем 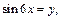 получим уравнение
получим уравнение 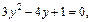 откуда
откуда 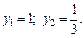
Приходим к совокупности простейших уравнений:
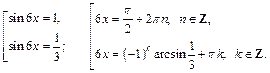
Получаем ответ:
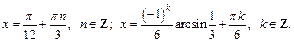
Пример 10.Найти сумму корней уравнения
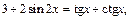 если
если 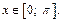
Решение. 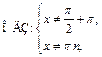 поскольку
поскольку 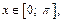
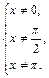
Упростим исходное уравнение:
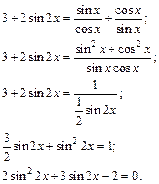
Получили квадратное уравнение относительно 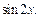 Сделав замену
Сделав замену 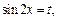 где
где 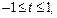 имеем уравнение
имеем уравнение 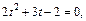 откуда
откуда 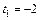 или
или 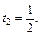
Вернувшись к прежней неизвестной, получим совокупность уравнений:
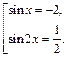
Первое уравнение не имеет решения. Решаем второе:
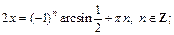
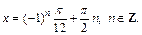
Придаем n значение n = 0, получаем:
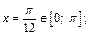
при n = 1 имеем 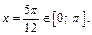
Нетрудно убедиться, что при всех других значениях n корни не попадут на отрезок 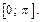 Значит сумма корней, принадлежащих отрезку
Значит сумма корней, принадлежащих отрезку 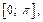 равна
равна
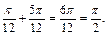
Получаем ответ: 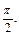
Дата добавления: 2015-09-29; просмотров: 809;
