Неоднородные уравнения 1-й степени
Неоднородным уравнением 1-й степени называется уравнение вида

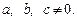 (7.29)
(7.29)
1-й способ решения. Используем формулы двойного аргумента:
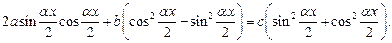
Тогда уравнение (7.29) сводится к однородному уравнению 2-й степени, которое решаем как уравнение (7.28).
2-й способ решения. Используем метод введения вспомогательного аргумента.
Разделив обе части уравнения (7.29) на  получим:
получим:
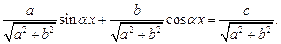
Так как  то существует угол j, такой, что
то существует угол j, такой, что
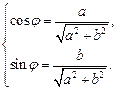 (7.30)
(7.30)
Тогда исходное уравнение (7.29) примет вид:
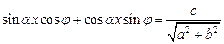
или, используя формулу (7.8) для синуса суммы, получим:
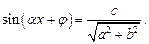
Если 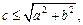 то последнее уравнение имеет решение:
то последнее уравнение имеет решение:
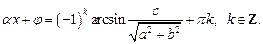
Угол j находят из формулы (7.30), например,
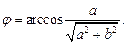
Приходим к ответу:
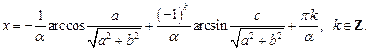
Пример 14.Решить уравнение 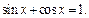
Решение.Разделив левую и правую часть уравнения на 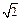 (так как
(так как  ), получим:
), получим:
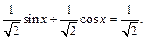
Тогда
 и
и 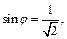
откуда
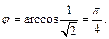
Таким образом, получаем уравнение:
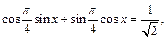

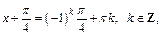
откуда приходим к ответу:

Дата добавления: 2015-09-29; просмотров: 1270;
