Формулы универсальной подстановки
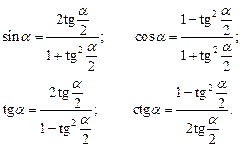 (7.15)
(7.15)
Пример 1.Упростить выражение 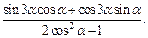
Решение.Используя формулы (7.7)–(7.9), получим:
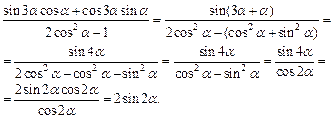
Пример 2.Вычислить выражение 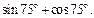
Решение. Чтобы применить формулы (7.12), преобразуем 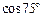 по формулам приведения:
по формулам приведения:
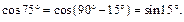
Тогда
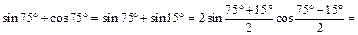
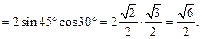
Пример 3.Вычислить выражение 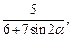 если
если 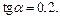
Решение.Используя универсальную подстановку, получим:
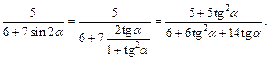
Подставив в полученное выражение 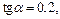 находим:
находим:
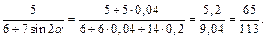
Пример 4.Преобразовать в произведение выражение
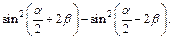
Решение.Для решения можно использовать формулы понижения степени, а также формулы суммы и разности тригонометрических функций (7.12) и (7.13):
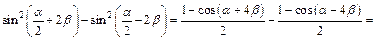
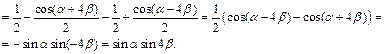
Пример 5. Найти значение выражения:
1) 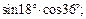
2) 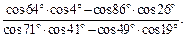
Решение. 1) Для применения формулы двойного аргумента 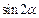 умножим и разделим исходное выражение на
умножим и разделим исходное выражение на 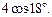 Получим:
Получим:
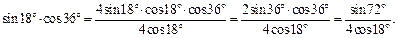
Используя формулы приведения, преобразуем
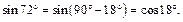
Тогда получим: 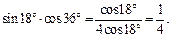
2) Из формул приведения следует:
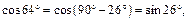
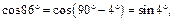
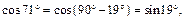
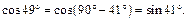
Отсюда, используя формулы (7.8), имеем:
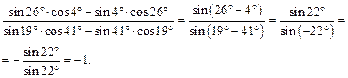
Дата добавления: 2015-09-29; просмотров: 1459;
