Основные тригонометрические тождества
 (7.4)
(7.4)
 (7.5)
(7.5)
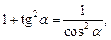 (7.6)
(7.6)
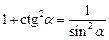 . (7.7)
. (7.7)
По значению одной из тригонометрических функций некоторого угла можно, используя приведенные выше формулы, найти значения всех остальных. Применение этих формул значительно упрощает процесс тригонометрических преобразований. При этом необходимо помнить, что при извлечении квадратного корня получаем выражение с модулем, например, 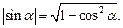 Раскрывая модуль, знак выбираем в зависимости от того, в какой четверти лежит угол
Раскрывая модуль, знак выбираем в зависимости от того, в какой четверти лежит угол 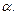
Пример 1. 1) Выразить в радианной мере угол, равный 150º.
2) Выразить в градусной мере угол в 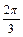 радиан.
радиан.
Решение. 1) Используя формулу (7.2), получим:

2) Используя формулу (7.3), получим:
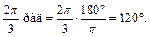
Пример 2.Вычислить tg a, если sin a = –0,8 и 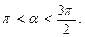
Решение. Сначала найдем cos a. Из формулы (7.4) получим:
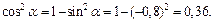
Так как в III четверти cos a < 0, то cos a = –0,6. Находим
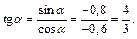
Пример 3.Вычислить 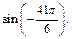
Решение.Используя нечетность и 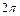 -периодичность функции
-периодичность функции  получаем:
получаем:
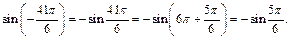
По формулам приведения находим:
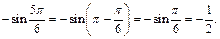
Таким образом, 
Пример 4.Определить знак выражения

Решение. Вначале используем нечетность функций, а затем их знаковые характеристики (рис. 7.6):
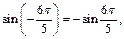
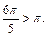
Следовательно, это угол III четверти, в которой синус принимает отрицательное значение (рис. 7.6). Тогда 
Угол 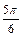 – это угол II четверти, в которой косинус отрицательный:
– это угол II четверти, в которой косинус отрицательный:
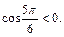
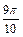 – это угол II четверти, тогда
– это угол II четверти, тогда 
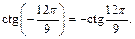
Угол 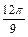 лежит в III четверти, тогда
лежит в III четверти, тогда  и
и 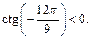
Учитывая знаки всех множителей, получаем:
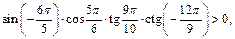
т. е. заданное выражение положительно.
Пример 5. Сравнить два числа  и
и 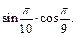
Решение. Заметим, что углы 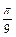 и
и 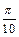 – это углы I четверти, в которой синус и косинус принимают положительные значения.
– это углы I четверти, в которой синус и косинус принимают положительные значения.
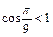 (в силу ограниченности функции косинус), тогда
(в силу ограниченности функции косинус), тогда
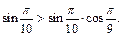
Пример 6. Указать наибольшее и наименьшее значения выражения 
Решение.Выражение будет наибольшим, если 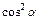 будет наибольшим.
будет наибольшим.
Известно, что 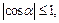 но тогда
но тогда 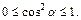
Тогда наибольшее значение выражения будет равно 2, если  а наименьшее равно –1, если
а наименьшее равно –1, если 
Дата добавления: 2015-09-29; просмотров: 754;
