Свойства тригонометрических функций
1. Знаковая характеристика тригонометрических функций следует из их определения через проекции на координатные оси (рис. 7.6).
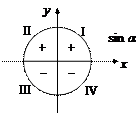 | 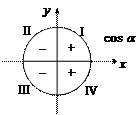 | 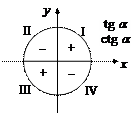 |
Рис. 7.6
2. Поскольку  и
и 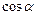 введены как проекции внутри единичной окружности, то для всякого угла
введены как проекции внутри единичной окружности, то для всякого угла 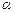 :
:

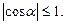
Функции 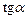 и
и 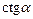 могут принимать любые по величине значения:
могут принимать любые по величине значения: 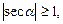

3. Функции 
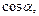
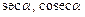 являются 2p-периодическими.
являются 2p-периодическими.
Функции 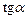 и
и 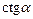 являются p-периодическими.
являются p-периодическими.
Следовательно, для тригонометрических функций выполняются следующие равенства:
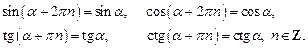
4. Функции 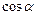 и
и  являются четными:
являются четными:

Функции 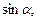
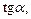
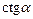 и
и 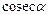 являются нечетными:
являются нечетными:

Значения тригонометрических функций некоторых углов приведены в табл. 7.1.
Т а б л и ц а 7.1
| Угол (a) | Функция | ||||
| градус | радиан | sin a | cos a | tg a | ctg a |
| 0º | не определен | ||||
| 30º | 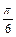
| 
| 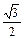
| 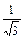
| 
|
| 45º | 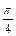
| 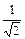
| 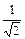
| ||
| 60º | 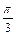
| 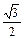
| 
| 
| 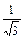
|
| 90º | 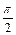
| не определен | |||
| 180º | 
| –1 | не определен | ||
| 270º | 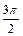
| –1 | не определен | ||
| 360º | 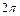
| не определен |
Правило приведения:
Функции  и
и 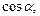
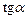 и
и 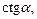
 и
и 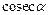 называются сходными друг для друга:
называются сходными друг для друга:
1. Если аргумент тригонометрической функции имеет вид:
а) 
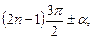
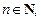
то функция меняется на сходную аргумента 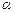 ;
;
б) 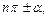
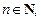
то сохраняется та же функция, но с аргументом 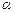 .
.
2. Перед функцией аргумента 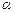 , записанной согласно пункту 1, ставится тот знак («+» или «–»), который имела исходная функция.
, записанной согласно пункту 1, ставится тот знак («+» или «–»), который имела исходная функция.
Всюду в преобразованиях по формулам приведения условно считают угол 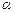 острым. В табл. 7.2 представлены формулы приведения.
острым. В табл. 7.2 представлены формулы приведения.
Т а б л и ц а 7.2
| x | 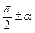
| 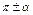
| 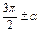
| 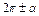
|
| sin x | 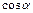
| 
| 
| 
|
| cos x | 
| 
| 
| 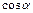
|
| tg x | 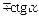
| 
| 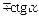
| 
|
| ctg x | 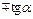
| 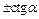
| 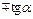
| 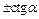
|
Дата добавления: 2015-09-29; просмотров: 790;
