Произвольного угла, их свойства

Тригонометрические функции

Рассмотрим систему координат Оху и в ней радиус-вектор

Будем рассматривать понятие угла с учетом направления поворота радиус-вектора от оси Ох. Если повернуть против движения часовой стрелки, то образованный этим радиус-вектором и положительным направлением оси Ох, назовем положительным углом (рис. 7.1).

Рис. 7.1

Если повернуть от оси Ох по ходу часовой стрелки, то образованный им будем называть отрицательнымуглом (рис. 7.1).

Если радиус-вектор повернуть от оси Ох в некотором направлении на часть полного оборота, то он образовал угол меры один градус ( ) в зависимости от направления поворота; часть от одного градуса называется минутой и обозначается 1'; часть от одной минуты называется секундой и обозначается 1''. Заданные единицы измерения вместе с направлением поворота дают возможность измерения любого угла, образованного радиус-вектором.

Кроме измерения угла в градусах используют также радианное измерение угла. Радианной мерой угланазывается отношение длины дуги, образованной поворотом конца радиус-вектора, к длине радиус-вектора с учетом направления поворота (рис. 7.2):

(7.1)

где l – длина дуги;

Рис. 7.2

Для перевода градусной меры в радианную и наоборот пользуются формулами:

(7.2)

(7.3)

В системе координат Оху рассмотрим единичную окружность с центром в начале системы координат и единичный радиус-вектор, образующий с осью Ох угол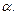

Спроецируем конец радиус-вектора на координатные оси, получим определенные точки (рис. 7.3). В прямоугольном треугольнике синусом острого угла называется отношение противолежащего катета к гипотенузе.

Рис. 7.3

Это понятие обобщается на любой угол острый и тупой, отрицательный и положительный.

Синусом угла 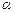называется проекция конца радиус-век­тора, образующего этот угол, на ось Оу:

Косинусом угла 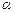называется проекция конца радиус-век­тора, образующего этот угол, на ось Ох:

Тангенсом угла 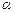называется величина, равная отношению синуса угла 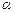к косинусу угла при условии

Котангенсом угла 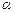называется величина, равная отношению косинуса угла 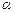к синусу угла при условии

Тангенс и котангенс угла 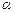можно определить также через проекции х и у:

Для того чтобы показать геометрический смысл 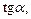построим ось тангенсов. Она проходит через точку (1; 0), касается единичной окружности, имеет такое же направление, как и ось Оу, и такой же масштаб на ней (рис. 7.4).

Рис. 7.4

Далее продолжаем радиус-вектор до пересечения с осью тангенсов. Полученный на оси тангенсов отрезок (с точностью до знаков) и является

Для того чтобы показать геометрический смысл 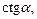рисуем ось котангенсов. Она проходит через точку (0; 1), имеет то же направление и тот же масштаб. Геометрическое значение 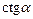получаем после того, как продолжим радиус-вектор до пересечения с осью котангенсов (рис. 7.5).

Рис. 7.5

Секансом угла 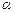называется величина

Косекансом угла 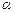называется величина