Методы определения порядка реакции

Определение порядка реакции открывает возможности выяснения вероятного механизма химического процесса. Для определения порядка реакции надо знать кинетические уравнения реакций различного порядка. В общем виде кинетическое уравнение реакции, например, первого порядка выглядит следующим образом: ,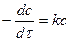

где с – концентрация исходного вещества, поэтому перед производной знак «–». После интегрирования этого уравнения, обозначив начальную концентрацию вещества через с₀, получим:

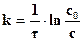(2.2)

Кинетическое уравнение реакции второго порядка, считая концентрации реагентов одинаковыми с₁=с₂=с, выглядит:

.

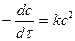Интегрируя это уравнение и обозначив через с₀ начальную концентрацию, получим:

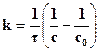(2.3.)

Экспериментально находят концентрации одного из веществ (с) через разные промежутки времени (t) от начала реакции. Значения (с) и начальной концентрации (с₀) подставляют в уравнение (2.2) и рассчитывают константу скорости. Если величина (k), вычисленная для разных моментов времени, остается практически постоянной, это говорит о том, что реакция первого порядка. Если значения (k) не сохраняют постоянного значения, то величины (с) и (с₀) подставляют в уравнение (2.3.) Постоянство значений (k) свидетельствует о втором порядке реакции.

Можно эти расчеты проделать графически. Из уравнения (2.2) следует, что график зависимости (lnc) от времени (t) должен иметь вид прямой линии. Действительно уравнение (2.2) можно записать как:

- .

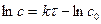Так как (-lnс₀) величина постоянная, то, обозначив ее через (В), получим:

-ln c=kt+B,

а это и есть уравнение прямой в координатах lnc-t. Полученные экспериментальные значения (с) наносят на график в этих координатах (рис. 2.1). Если получается прямая линия, то реакция имеет первый порядок. Тангенс угла наклона этой прямой (tga) равен k, а отрезок, отсекаемый ею на оси ординат равен ln с₀.

Из уравнения (2.3) следует, что зависимость 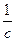от t выражается прямой линией, так как это уравнение можно представить в виде:

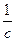=kt + В, где В= .

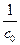Если экспериментальные точки в координатах lnc-t не ложатся на прямую линию, то строят график в координатах 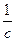–t (рис. 2.2). Если получается прямая линия, то реакция второго порядка, а тангенс угла наклона прямой по отношению к оси абсциссе (tg a) равен (k). Отрезок, отсекаемый прямой не оси ординат, равен .

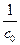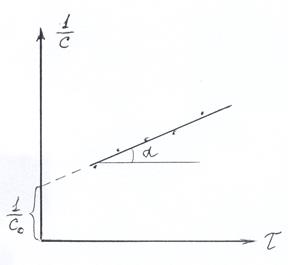
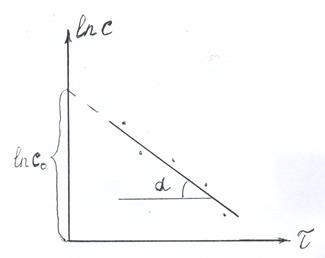
Рис. 2.1 Рис. 2.2

Порядок реакции можно определять по периоду полупревращения. Периодом полупревращения называется время, в течение которого в реакцию вступит половина исходного количества вещества.

Подставив в уравнение (2.2) величину 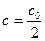, получим:

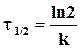. (2.4).

Т.е. период полупревращения реакции первого порядка связан только с величиной константы скорости (k) и не зависит от начальной концентрации вещества.

Для реакции второго порядка, подставив в уравнение (2.3) величину 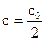, получим:

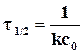(2.5).

Таким образом, для реакции второго порядка период полупревращения уменьшается с увеличением начальной концентрации реагентов.

Для определения порядка реакции проводят реакцию при различных начальных концентрациях вещества (с₀) и определяют период полупревращения. Если реакция имеет первый порядок, то период полупревращения при разных (с₀) будет одним и тем же. Если период полупревращения обратно пропорционален начальной концентрации, реакция имеет второй порядок. Зная порядок реакции, можно рассчитать константу скорости по уравнениям (2.4) или (2.5).