Принцип Ландауэра

Преобразование информации связано с затратой энергии. Найдем минимальную энергию, необходимую для стирания или для получения бита информации.

Рассмотрим ящик, содержащий одну частицу и имеющий в середине съемную перегородку, показанную на рис. 2.12, а. Частица находится в левой половине ящика. Далее перегородка вынимается, что соответствует рис. 2.12, б. Найдем изменение энтропии системы и минимальное количества энергии, связанной с этим процессом.

Для изолированных объемов фазовое пространство системы распадается на независимые подпространства. Формула Больцмана для энтропии (2.101)

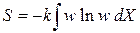
получает вид

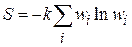, (П.3.16)

где 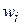– вероятность обнаружения частицы в объеме с номером i. Соответствующие вероятности приведены на рисунке.

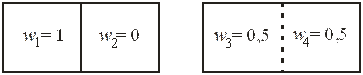
а б

Рис. 2.12. Частица в сосуде с перегородкой (а), и без нее (б)

Для состояний на рис. 2.12 а и б находим

,

.

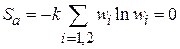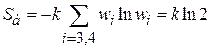При изотермическом переходе между состояниями увеличение энтропии пропорционально количеству рассеянного тепла

,

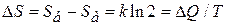откуда

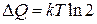. (П.3.17)

Состояние а соответствует биту информации о частице в системе. Переход к состоянию б приводит к потере этой информации. В результате выполняется принцип Ландауэра (1961 г.)– стирание бита информации приводит к рассеянию энергии 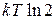в окружающую среду с температурой Т. При 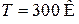получаем 0,0178 эВ. Другие формулировки для

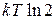
– энергия, затрачиваемая на создание бита информации;

– высота барьера, необходимая для разделения двух состояний электрона, или другого носителя информации;

– нижний предел для энергии реального процесса преобразования информации, как показано экспериментально (Nature (2012) 483, 187).

С учетом огромного количества преобразуемой компьютером информации результат (П.3.17) имеет важные технические приложения, поэтому получил собственное имя.

До Ландауэра результат (П.3.17) получил в 1949 г. фон Нейман – американский математик, заложивший принципы работы компьютера и математические основы квантовой механики.

Рольф Ландауэр (1927–1999) Джон фон Нейман (1903–1957)