Статистический интеграл поступательного движения
Идеальный газ из N микрочастиц находится в объеме V при температуре Т. Найдем статистический интеграл поступательного движения, внутреннюю энергию и давление газа.
1. Статистический интеграл частицы
Используем
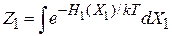 ,
,
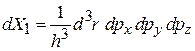 ,
,
и гамильтониан поступательного движения материальной точки
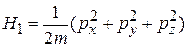 .
.
Подстановка дает
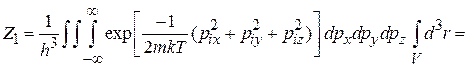
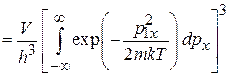 .
.
Учтено, что координаты и разные проекции импульса разделены. Использовано
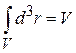 .
.
Последний интеграл в квадратных скобках является интегралом Пуассона
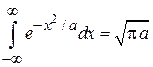 ,
,
и равен 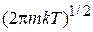 . Получаем статистический интеграл поступательного движения частицы (2.22)
. Получаем статистический интеграл поступательного движения частицы (2.22)
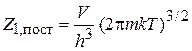 . (П.3.1)
. (П.3.1)
С учетом
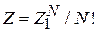
находим статистический интеграл поступательного движения газа
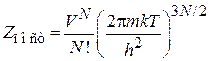 .
.
2. Внутренняя энергия газа
Вычисляем (2.26)
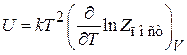 .
.
Из 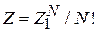 находим
находим
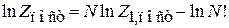 ,
,
тогда
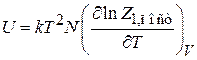 , (П.3.1а)
, (П.3.1а)
средняя энергия частицы
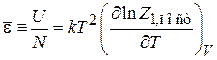 . (П.3.1б)
. (П.3.1б)
Выполняется
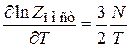 ,
,
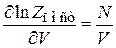 . (П.3.1в)
. (П.3.1в)
Действительно, из
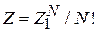 ,
, 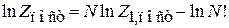 ,
,
находим
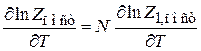 ,
,
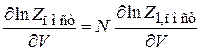
С учетом (П.3.1)
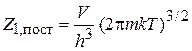 ,
,
получаем (П.3.1в).
Из (П.2.26)
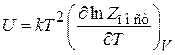
и (П.3.1в)
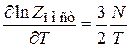
получаем
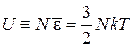 ,
,
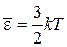 .
.
Результат совпадает с выражением, найденным из микроканонического распределения, а также с известной формулой термодинамики идеального газа.
3. Давление газа
Из (2.98)
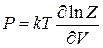
и (П.3.1в)
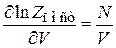
находим
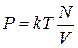
и получаем уравнение идеального газа 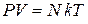 .
.
Дата добавления: 2015-09-21; просмотров: 770;
