Определение скорости точки при координатном способе задания её движения
Пусть движение точки задано координатным способом в декартовой системе координат
х = x(t), y = y(t), z = z(t)
Радиус-вектор точки равен
.
Так как единичные векторы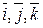 
постоянны, то по определению
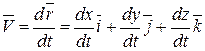. (5.12)
Обозначим проекции вектора скорости на оси Ох, Оу и Oz через Vx, Vy, Vz соответственно и разложим вектор скорости по осям:
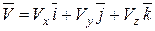(5.13)
Сравнивая равенства (5.12) и (5.13) получим
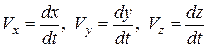(5.14)
В дальнейшем производную по времени будем обозначать точкой сверху, т.е.
.
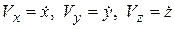Модуль скорости точки определяется формулой
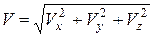. (5.15)
Направление вектора скорости определяется направляющими косинусами:
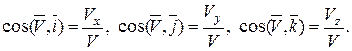
Дата добавления: 2015-09-21; просмотров: 540;