Определение скорости и ускорения точки при естественном способе задания её движения
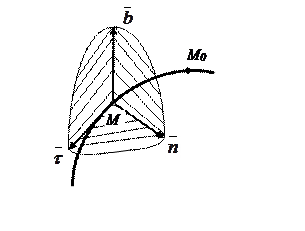 Рис.5.12
Рис.5.12
| При этом способе используются естественные оси с началом в текущем положении точки М на траектории (рис.5.12) и единичными векторами 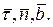 Единичный вектор Единичный вектор 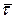 направлен по касательной к траектории в сторону положитель- ного отсчета дуги, единичный вектор направлен по касательной к траектории в сторону положитель- ного отсчета дуги, единичный вектор 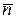 направлен по главной нормали траектории в сторону ее вогнутости, единичный вектор направлен по главной нормали траектории в сторону ее вогнутости, единичный вектор 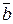 направлен по бинормали к траектории в точке М. направлен по бинормали к траектории в точке М.
|
Орты 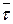 и
и 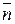 лежат в соприкасающейся плоскости, орты
лежат в соприкасающейся плоскости, орты 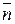 и
и 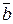 в нормальной плоскости, орты
в нормальной плоскости, орты 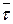 и
и 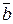 - в спрямляющей плоскости.
- в спрямляющей плоскости.
Полученный трехгранник называется естественным.
Пусть задан закон движения точки s = s(t).
Радиус вектор 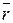 точки М относительно какой-либо фиксированной точки будет сложной функцией времени
точки М относительно какой-либо фиксированной точки будет сложной функцией времени 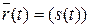 .
.
Из дифференциальной геометрии известны формулы Серре-Френе, устанавливающие связи между единичными векторами естественных осей и вектор-функцией кривой
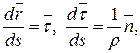
где r - радиус кривизны траектории.
Используя определение скорости и формулы Серре-Френе, получим:
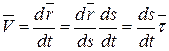 . (5.20)
. (5.20)
Обозначая проекцию скорости на касательную 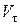 и учитывая, что вектор скорости направлен по касательной, имеем
и учитывая, что вектор скорости направлен по касательной, имеем
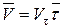 . (5.21)
. (5.21)
Сравнивая равенства (5.20) и (5.21), получим формулы для определения вектора скорости по величине и направлению
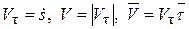 . (5.22)
. (5.22)
Величина 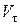 положительна, если точка М движется в положительном направлении отсчета дуги s и отрицательна в противоположном случае.
положительна, если точка М движется в положительном направлении отсчета дуги s и отрицательна в противоположном случае.
Используя определение ускорения и формулы Серре-Френе, получим:
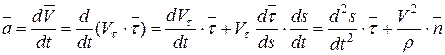 (5.23)
(5.23)
Обозначим проекцию ускорения точки 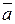 на касательную
на касательную 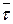 , главную нормаль и бинормаль
, главную нормаль и бинормаль 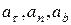 соответственно.
соответственно.
Тогда ускорение равно
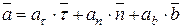 (5.24)
(5.24)
Из формул (5.23) и (5.24) следует, что вектор ускорения всегда лежит в соприкасающейся плоскости и раскладывается по направлениям 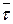 и
и 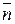 :
:
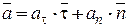 (5.25)
(5.25)
Проекция ускорения на касательную 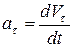 называется касательным или тангенциальным ускорением. Оно характеризует изменение величины скорости.
называется касательным или тангенциальным ускорением. Оно характеризует изменение величины скорости.
Проекция ускорения на главную нормаль 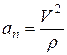 называется нормальным ускорением. Оно характеризует изменение вектора скорости по направлению.
называется нормальным ускорением. Оно характеризует изменение вектора скорости по направлению.
Модуль вектора ускорения равен 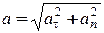 .
.
Если 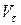 и
и 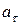 одного знака, то движение точки будет ускоренным.
одного знака, то движение точки будет ускоренным.
Если 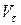 и
и 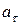 разных знаков, то движение точки будет замедленным.
разных знаков, то движение точки будет замедленным.
Дата добавления: 2015-09-21; просмотров: 1289;
