Ускорение точки
Пусть теперь известна функция 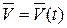 . На рис. 5.10
. На рис. 5.10 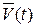 и
и 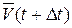 - векторы скорости движущейся точки в моменты t и Dt. Чтобы получить приращение вектора скорости
- векторы скорости движущейся точки в моменты t и Dt. Чтобы получить приращение вектора скорости 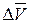 перенесем параллельно вектор
перенесем параллельно вектор 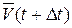 в точку М:
в точку М:
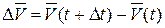
Средним ускорением точки за промежуток времени Dt называется отношение приращения вектора скорости 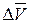 к промежутку времени Dt:
к промежутку времени Dt:
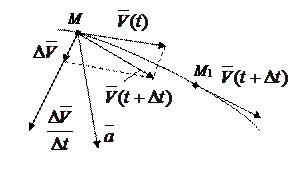 Рис.5.10 Рис.5.10
| 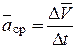 .
Ускорением .
Ускорением 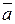 точки в данный момент времени называется предел отношения приращения скорости точки в данный момент времени называется предел отношения приращения скорости 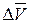 к приращению времени Dt при стремлении последнего к нулю, т.е. к приращению времени Dt при стремлении последнего к нулю, т.е.
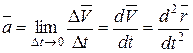 . .
|
Следовательно, ускорение точки в данный момент времени равно первой производной по времени от вектора скорости точки или второй производной радиус-вектора по времени
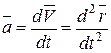 . (5.11)
. (5.11)
Ускорение точки - это векторная величина, характеризующая быстроту изменения вектора скорости по времени.
Построим годограф скорости (рис.5.11). Годографом скорости по определению является кривая, которую вычерчивает конец вектора скорости при движении точки, если вектор скорости откладывается из одной и той же точки.
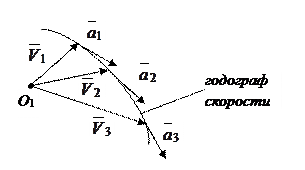 Рис.5.11
Рис.5.11
| Очевидно, что скорость точки, вычерчивающей годограф скорости, будет равна ускорению точки при ее движении по траектории. Единицей измерения ускорения в системе Си является м/с2. |
Дата добавления: 2015-09-21; просмотров: 603;
