Способ отыскания момента силы относительно точки

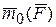Найдем формулу, выражающую вектор . Рассмотрим векторное произведение 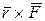. По определению векторного произведения векторы 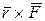и 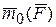совпадают по направлению.

Определим модуль вектора :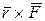

.

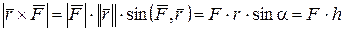Таким образом, векторы 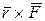и 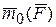совпадают по величине и по направлению

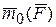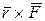= (2.1)

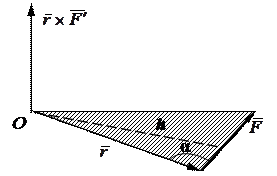
Момент силы относительно произвольной точки пространства О равен векторному произведению радиуса-вектора точки приложения силы

относительно точки О на саму силу.

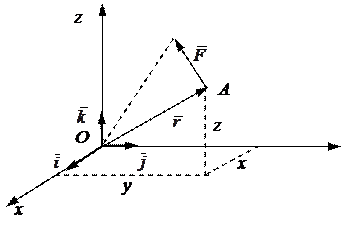Вспомним из векторной алгебры как можно представить векторное произведение, если заданы векторы 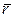и 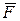. В декартовой системе координат представим векторы

,

.

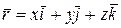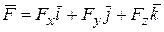Рис.2.3

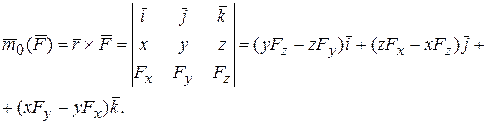(2.2)

В формуле (2.2) коэффициенты при ортах 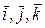- это проекции момента силы на оси х, у, z:

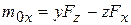
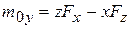(2.3)

.

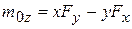Значит можно найти модуль момента

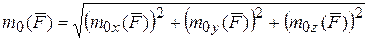. (2.4)

Чтобы вектор полностью определить, можно найти его направляющие косинусы:

, ,

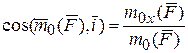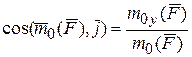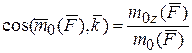. (2.5)

Некоторые свойства момента силы относительно точки:

1) момент силы относительно точки не изменяется при переносе точки приложения силы вдоль ее линии действия;

2) момент силы относительно точки равен нулю, когда а) F=0; б) h=0,

То есть когда точка О расположена на линии действия силы.