Этой оси

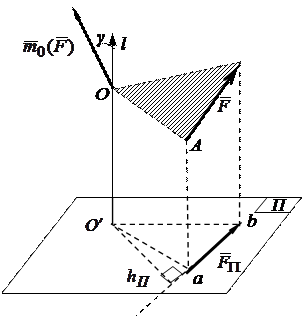
Пусть даны сила 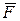и ось l. Возьмем произвольную точку О на оси l и найдем вектор 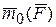(рис. 2.5). Обозначим γ угол, который составляет вектор 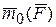с осью l. Возьмем другую точку 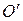на оси l и проводим через нее плоскость П перпендикулярную оси l. Спроектируем силу 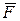на плоскость П. Из геометрии известно, что если нормали к двум плоскостям составляют угол γ, то и плоскости составляют этот угол и для площадей треугольников справедлива формула:

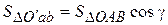. (2.8)

Домножим формулу (2.8) на два:

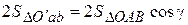. (2.9)

В формуле (2.9)

,

.

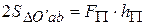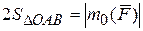Следовательно

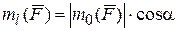или

.

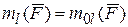Рис. 2.5

Момент силы относительно оси равен проекции на эту ось момента силы относительно любой точки этой оси.