Умножение матриц
Число столбцов матрицы A должно быть равно числу строк матрицы B, тогда говорят, что эти две матрицы согласуются по форме, и произведение AB существует. Если матрица A имеет размерность (m×n), а матрица B имеет размерность (n×k), то матрица C, являющаяся результатом произведения AB=C, будет иметь размерность (m×k). Условно это обозначим так:
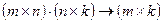 .
.
Для матриц A (m×n) и B (n×m) существует как произведение AB, так и произведение BA. Произведение AB имеет размерность (m×m), а произведение BA - размерность (n×n). Естественно, что они в общем случае не равны. Даже в случае m=n, а значит, при одинаковой размерности (m×m) произведений AB и BA, эти произведения не обязательно равны. Если же оказывается, что они равны, т.е. AB=BA, то в этом случае говорят, что матрицы коммутативны.
Пример 3. Вычислить произведения указанных матриц:
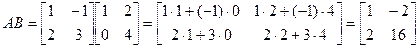 ;
;
 .
.
Свойства умножения матриц. Умножение в общем случае не коммутативно, ассоциативно и дистрибутивно.
1. Некоммутативность:
AB≠BA.
2. Ассоциативность:
(AB)C=A(BC).
3. Дистрибутивность:
(A+B)C=AC+BC.
Умножение на скаляр.
При умножении на скалярную величину каждый элемент матрицы умножается на него.
Умножение на диагональную матрицу.
Умножение слева матрицы A на диагональную матрицу D эквивалентно операции эквивалентную операции со строками A. При умножении справа матрицы A на диагональную матрицу D операции производятся со столбцами матрицы A.
Умножение транспонированных матриц(транспонирование произведения матриц):
(A∙B)T = BT∙AT.
Умножение на единичную матрицу.
Умножение как слева, так и справа на единичную матрицу не изменяет исходную матрицу, т.е.
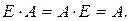
Дата добавления: 2015-09-18; просмотров: 898;
