Статистический анализ временных рядов

Вкратце рассмотрим традиционные подходы к статистическому анализу временных рядов. Исторически центральное место в статистическом анализе временных рядов занимали линейные модели АRМА. Со временем эта область оформилась в законченную теорию с набором методов – теорию Бокса-Дженкинса. В этом подходе модель задается двумя компонентами, характеризующими авторегрессию и скользящее среднее. Общая формула для процесса с авторегрессией и скользящим средним порядка (р,q) имеет вид:

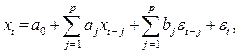(2.2)

где р – порядок авторегрессии (положительное целое число), q – порядок скользящего среднего, e_t – шум (некоррелированный временной ряд, подчиненный гауссову распределению с нулевым средним и дисперсией 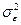). Коэффициенты а_j и b_j; являются параметрами модели. Если q=0, то получается авторегрессионная модель АR(р), а если р=0, – модель скользящего среднего МА(q).

Присутствие в модели АRМА авторегрессионного члена выражает то обстоятельство, что текущие значения переменной зависят от ее прошлых значений. Такие модели называются одномерными. Часто, однако, значения исследуемой целевой переменной связаны с несколькими разными временными рядами. Так будет, например, если целевая переменная — курс обмена валют, а другие участвующие переменные – процентные ставки (в каждой из двух валют). Соответствующие методы называются многомерными. Общий вид уравнения многомерной модели такой:

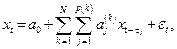(2.3)

где k – номер временного ряда (всего их – N). Математическая структура линейных моделей довольно проста, и расчеты по ним могут быть без особых трудностей выполнены с помощью стандартных пакетов численных методов. Следующим шагом в анализе временных рядов стала разработка моделей, способных учитывать нелинейности, присутствующие, как правило, в реальных процессах и системах. Одна из первых таких моделей была предложена Тонгом и называется пороговой авторегрессионной моделью (ТАR). В ней, при достижении определенных (установленных заранее) пороговых значений, происходит переключение с одной линейной АR-модели на другую. Тем самым в системе выделяется несколько режимов работы. Через 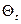, обозначим номер режима в момент t ( 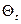=1,2,...,r). Тогда одномерная АR-модель с соответствующим номером дает:

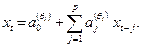(2.4)

Затем были предложены STAR-, или «гладкие» ТАR-модели. Такая модель представляет собой линейную комбинацию нескольких моделей, взятых с коэффициентами, которые являются непрерывными функциями времени. Примером может служить следующее уравнение модели, в котором Q – гладкая функция, принимающая значения от 0 до 1:

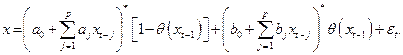(2.5)