Предварительная обработка данных

При моделировании реальных процессов «чистые» данные – это редкая роскошь. В силу самой своей природы, реальные данные содержат шумы и бывают неравномерно распределены. Очень часто практик просто собирает данные и подает их на вход модели, надеясь, что все получится. Однако, при сетевом подходе (и это верно здесь даже в большей степени, чем для классического статистического анализа) тщательная предварительная обработка данных может сэкономить массу времени и уберечь от многих разочарований. Рассмотрим следующие относящиеся сюда вопросы: сбор данных; их анализ и очистку; их преобразование с целью сделать входную информацию более содержательной и удобной для сети.

Сбор данных

Самое важное решение, которое должен принять аналитик – это выбор совокупности переменных для описания моделируемого процесса. Чтобы представить себе возможные связи между разными переменными, нужно хорошо понимать существо задачи. В этой связи очень полезно будет побеседовать с опытным специалистом в данной предметной области. Относительно выбранных вами переменных нужно понимать, значимы ли они сами по себе, или же в них всего лишь отражаются другие, действительно, существенные переменные. Проверка на значимость включает в себя кросс-корреляционный анализ. С его помощью можно, например, выявить временную связь типа запаздывания (лаг) между двумя рядами. То, насколько явление может быть описано линейной моделью, проверяется с помощью регрессии по методу наименьших квадратов (OLS).

Полученная после оптимизации невязка R² может принимать значения от 0 (полное несоответствие) до 1 (точное соответствие). Часто бывает так, что для линейных систем OLS-метод дает такие результаты, которые уже нельзя сколько-нибудь значительно улучшить применением нейронных сетей.

В целом, можно сказать, что предварительная обработка через формирование совокупности переменных и проверку их значимости существенно улучшает качество модели. Если никаких теоретических методов проверки в распоряжении нет, переменные можно выбирать методом проб и ошибок, или с помощью формальных методов типа генетических алгоритмов.

Очистка и преобразование базы данных

Стоит начать с того, чтобы изобразить распределение переменной с помощью гистограммы или же рассчитать для него характеристики асимметрии (симметричность распределения) и эксцесса (весомости «хвостов» распределения). В результате будет получена информация о том, насколько распределение данных близко к нормальному. Многие методы моделирования, в том числе, – нейронные сети, дают лучшие результаты на нормализованных данных. Далее, с помощью специальных статистических тестов, например, на расстояние Махаланобиса, можно выявить многомерные выбросы, с которыми затем нужно разобраться на предмет достоверности соответствующих данных. Эти выбросы могут порождаться ошибочными данными или крайними значениями, вследствие чего структура связей между переменными может (а может и не) нарушаться. В некоторых приложениях выбросы могут нести положительную информацию, и их не следует автоматически отбрасывать.

Предварительное, до подачи на вход сети, преобразование данных с помощью стандартных статистических приемов может существенно улучшить как параметры обучения (длительность, сложность), так и работу системы.

Для того чтобы улучшить информационную структуру данных, могут оказаться полезными определенные комбинации переменных – произведения, частные и т.д. Например, когда вы пытаетесь предсказать изменения цен акций по данным о позициях на рынке опционов, отношение числа опционов пут (put options, т.е. опционов на продажу) к числу опционов колл (call options, т.е. опционов на покупку) более информативно, чем оба этих показателя в отдельности. К тому же, с помощью таких промежуточных комбинаций часто можно получить более простую модель, что особенно важно, когда число степеней свободы ограниченно.

Наконец, для некоторых функций преобразования, реализованных в выходном узле, возникают проблемы с масштабированием. Сигмоид определен на отрезке [0,1], поэтому выходную переменную нужно масштабировать так, чтобы она принимала значения в этом интервале. Известно несколько способов масштабирования: сдвиг на константу, пропорциональное изменение значений с новым минимумом и максимумом, центрирование путем вычитания среднего значения, приведение стандартного отклонения к единице, стандартизация (два последних действия вместе). Имеет смысл сделать так, чтобы значения всех входных и выходных величин в сети всегда лежали, например, в интервале [0,1] или [-1,1], – тогда можно будет без риска использовать любые функции преобразования.

Еще одна важная проблема (которая одновременно является основным преимуществом нейронно-сетевых методов) – способность работать с данными качественного характера. Отношения эквивалентности или порядка нужно суметь записать для входа (или выхода) сети. Это можно сделать, вводя искусственные переменные, принимающие значения 1 или 0.

Построение модели

Значения целевого ряда (это тот ряд, который нужно найти, например, доход по акциям на день вперед) зависят от N факторов, среди которых могут быть комбинации переменных, прошлые значения целевой переменной, закодированные качественные показатели. Эти факторы определяются обычными методами статистики (метод наименьших квадратов, кросс-корреляция и т.д.). Входные и выходные переменные преобразуются (масштабированием, стандартизацией) так, чтобы они принимали значения от 0 до 1 (или от -1 до 1). В результате получаем первоначальную модель, которую можно пытаться оптимизировать с помощью нейронной сети.

Необходимо или прямо указать размеры сети (число скрытых слоев, скрытых элементов, структуру связей), или настроить модель на имеющиеся данные, применяя конструктивный либо деструктивный подход (например, уменьшение весов).

Оптимизация обучения

На протяжении всего процесса оптимизации следует проверять, согласуется ли работа модели на обучающем множестве с соответствующими результатами на подтверждающем множестве.

Статическое и адаптивное обучение

При моделировании финансовых временных рядов вопрос о том, как разбить все имеющиеся данные на обучающее, подтверждающее и тестовое множества, является нетривиальным. Например, если данные, касающиеся биржевого краха, отнести к подтверждающему множеству, это даст искаженные результаты. При статическом подходе обычно поступают так: берут два небольших промежутка времени до и после обучающего множества и из них случайным образом выбирают образцы в подтверждающее множество. Никогда не будет лишним проверить, насколько изменятся результаты, если множество выбрать иначе.

Изменчивый характер финансовых рынков плохо согласуется с долгосрочными моделями устойчивости. Под действием краткосрочных «модных» тенденций или паники на бирже может существенно измениться реакция людей на те или иные показатели рынка. Чтобы справиться с этой трудностью, были предложены так называемые адаптивные нейронные сети, в которых веса модели непрерывно уточняются с помощью процедуры обучения на все новых временных промежутках.

Отбор и диагностика модели

Проверка свойств модели временного ряда – необходимое условие для надежного предсказания и для понимания природы имеющихся закономерностей. К сожалению, этот вопрос слабо освещен в литературе.

Разности между истинными и оцененными значениями должны подчиняться гауссовскому распределению с нулевым средним. Если оказалось, что распределение имеет слишком тяжелые хвосты или несимметрично, то нужно пересмотреть модель. Среди значений разностей могут выявиться закономерности или последовательные корреляции, тогда необходимо дополнительное обучение или улучшение модели.

Оценка качества модели обычно основывается на критерии согласия типа средней квадратичной ошибки (MSE) или квадратного корня из нее (RMSE). Эти критерии показывают, насколько предсказанные значения оказались близки к обучающему, подтверждающему или тестовому множествам. Для рядов с большим разбросом Лапедес предложил критерий средней относительной вариации:

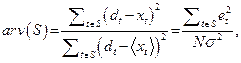(2.6)

где S — временной ряд, е_t – разность (истинное значение d_t минус х_t) в момент t, 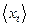– оценка для среднего значения ряда, N – число данных в ряде. Последующая нормализация с помощью оценки для вариации позволяет проводить более надежные сравнения для различных приложений.

Используя предыдущее значение х_t-1 целевой переменной, можно оценить способность модели предсказывать на один шаг вперед. Подставляя предсказанные значения на место истинных, получим метод предсказания на k шагов вперед. Если через несколько шагов модель начинает отклоняться от настоящей траектории, это значит, что в ней происходит накопление и рост ошибки.

Самый распространенный метод выбора нейронно-сетевой модели с наилучшим обобщением — это проверка критерия согласия (MSE, ARV и др.) на тестовом множестве, которое не использовалось при обучении. Если же данных мало, разбивать их на обучающее и подтверждающее множество нужно разными способами. Такое перекрестное подтверждение может потребовать много времени, особенно для нейронных сетей с их длительным процессом обучения.

В линейном анализе временных рядов можно получить несмещенную оценку способности к обобщению, исследуя результаты работы на обучающем множестве (MSE), число свободных параметров (W) и объем обучающего множества (N). Оценки такого типа называются информационными критериями (IC) и включают в себя компоненту, соответствующую критерию согласия, и компоненту штрафа, которая учитывает сложность модели. Барроном [30] были предложены следующие информационные критерии: нормализованный IC Акаике (NAIC), нормализованный байесовский IC (NBIC) и итоговая ошибка прогноза (FPE):

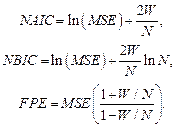(2.7)

FPE представляет собой несмещенную оценку способности к обобщению для нелинейных моделей, в частности, – для нейронных сетей. К сожалению, при этом предполагается, что в нашем распоряжении имеется бесконечное число наблюдений, – в этом случае оценка надежности модели, вообще, не представляет особых сложностей.

Ясно, что информационные критерии дают информацию об адекватности модели и помогают выбрать модель подходящего уровня сложности. Другие методы диагностики позволяют, если такая задача стоит, избежать подхода к системе как к «черному ящику». Поскольку основное отличие сети от линейной регрессии — это возможность применять нелинейные преобразователи, имеет смысл посмотреть, насколько глубоко модель использует свои нелинейные возможности. Проще всего это сделать с помощью введенного Вигендом отношения:

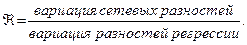(2.8)

Для более тщательной проверки нелинейных возможностей нужно изобразить распределение выходных значений для скрытых элементов. Слишком большая доля крайних значений (0 или 1) говорит о том, что некоторые элементы попали в режим насыщения. Еще один способ – построить совместное распределение линейного и нелинейного выходов и применить линейную регрессию. Отклонения от наклона с углом 45° говорят о том, что нелинейные возможности задействованы. Между прочим, встречается точка зрения, что появление во время обучения резких изменений разностей говорит об использовании нелинейностей. К сожалению, это не соответствует действительности.

Следует также проверить, скоррелированны ли действия скрытых элементов. В многомерном регрессионном анализе при росте мультиколлинеарности значения коэффициентов регрессии становятся все менее надежными. Так же и здесь предпочтительно, чтобы выходы скрытых элементов одного слоя были некоррелированны. Нужно найти собственные значения корреляционной матрицы для выходов скрытых узлов по данным обработки всех обучающих примеров. При полной некоррелированности все собственные значения будут равны единице, а отличия от единицы говорят об избыточном числе скрытых элементов.

Доводка

При построении системы прогноза преследуется цель не только расширить наше понимание процессов, но и получить помощь для принятия решений в финансовой области. Такого рода руководства можно создать с помощью комбинаций нескольких нейронных сетей, обученных на разных множествах данных и разных отрезках времени. Например, сигналы на покупку или продажу будут даваться по пороговым значениям, которые настроены с учетом предыдущих позиций и ошибок. Очень важно также распознать момент, когда эффективность модели начинает падать.