База данных и предварительная обработка

Имеются данные измерений для 150 экземпляров ирисов, в равных частях (по 50 штук) принадлежащих к трем видам (iris setosa, iris versicolor, iris virginica). Для каждого экземпляра ириса известны 4 величины: длина чашелистика (SL), ширина чашелистика (SW), длина лепестка (PL) и ширина лепестка (PW). На рис. 2.3показан представительный срез базы данных. Входной файл для нейронной сети состоит из 150 строк (по 50 для каждого сорта):

• первые 4 переменные — длина чашелистика (SL), ширина чашелистика (SW), длина лепестка (PL) и ширина лепестка (PW).

• пятая переменная — целевая, обозначает класс (вид) и для различных видов принимает следующие значения: 0 – setosa, 0.5 – versicolor, 1 – virginica. Такой способ кодировки связан с предположением Фишера, что versicolor – это гибрид setosa и virginica. На срезе PW/PL (рис. 2.3) можно заметить соответствующую упорядоченность. Здесь можно было бы использовать и другой метод кодировки, например разбить задачу на три подзадачи с двумя классами каждая.

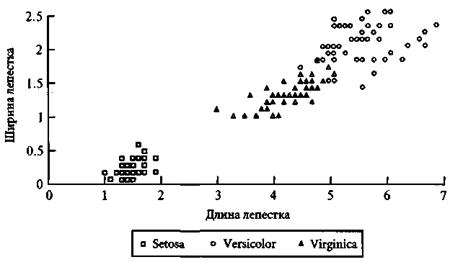
Рис. 2.3. Ирисы Фишера. Двумерная проекция массива данных (ширина и длиналепестка)

Обучение и доводка

На этой задаче были опробованы три различные конфигурации сети. Все сети имели четыре входных узла, количество скрытых элементов менялось от трех до пяти, выходной узел был во всех случаях один. В качестве отображающей функции для каждого узла был взят простой сигмоид, принимающий на выходе значения от 0 до 1. Образец относился к тому или иному классу согласно простому пороговому правилу интерпретации выхода сети: выход > 2/3 ® virginica; выход < 1/3 ® setosa; остальные значения ® versicolor.

Обучение было проделано с помощью пакета Nevada Quick Prop на майнфрейм - компьютере Convex. Никакой оптимизации процесса обучения не производилось: процесс заканчивался, когда средняя квадратичная ошибка переставала существенно уменьшаться за 1000 итераций (эпох). Коэффициент, определяющий длину шага, во всех случаях принимался равным 0.1, а начальные значения весов брались случайным образом в интервале [-0.1,0.1]. Обучение занимало 10000-30000 эпох в зависимости от сложности сети. Полученные в результате значения весов приведены в верхнем левом углу таблицы на рис. 2.7 (см. ниже). В частности, значения веса третьего скрытого элемента и выходного узла равны, соответственно, 48.65 и 0.69. Вес соединения, идущего от первого скрытого элемента к выходному, равен 4.16.

Результаты

В табл. 2.1 приведены результаты для сетей в сравнении с другими известными методами. Следует при этом помнить, что невязка при повторной подстановке дает несколько приукрашенную картину для точности метода. Особенно это относится к самой большой сети, на которой достигнуто полное распознавание.

Таблица 2.1

Результаты классификации для задачи с ирисами Фишера