Нейронная сеть с прямой связью как классификатор

Поскольку сети с прямой связью являются универсальным средством аппроксимации функций, с их помощью можно оценить апостериорные вероятности в данной задаче классификации. Благодаря гибкости в построении отображения можно добиться такой точности аппроксимации апостериорных вероятностей, что они практически будут совпадать со значениями, вычисленными по правилу Байеса так называемые оптимальные процедуры классификации,.

Богатые возможности отображения особенно важны в тех случаях, когда на основе нескольких оценок строится высокоуровневая процедура принятия решений. Известно много приложений нейронных сетей с прямой связью к задачам классификации. Как правило, они оказываются эффективнее других методов, потому что нейронная сеть генерирует бесконечное число нелинейных регрессионных моделей.

К сожалению, хотя теоретически характеристики нейронной сети с прямой связью стремятся к байесовской, в применении их к практическим задачам выявляется ряд недостатков. Во-первых, заранее неизвестно, какой сложности (т.е. размера) сеть потребуется для достаточно точной реализации отображения. Эта сложность может оказаться чрезмерно большой. Архитектура сети, т.е. число слоев и число элементов в каждом слое, должна быть зафиксирована до начала обучения. Эта архитектура порождает сложные нелинейные разделяющие поверхности в пространстве входов. В сети с одним скрытым слоем векторы образцов сначала преобразуются (нелинейным образом) в новое пространство представлений (пространство скрытого слоя), а затем гиперплоскости, соответствующие выходным узлам, располагаются так, чтобы разделить классы уже в этом новом пространстве. Тем самым, сеть распознает уже другие характеристики – «характеристики характеристик», полученные в скрытом слое.

Все это подчеркивает важность этапа предварительной обработки данных. Чем более компактно представлены характеристики образцов, тем меньше зависимость от настраиваемых параметров сети (0 или 1).

Кодирование на выходе

Задача двоичной классификации может быть решена на сети с одним выходным элементом, который может находиться в состоянии 0 или 1. Для задачи с многими классами нужно разработать способ записи (кодирования) выхода. Один возможный способ состоит в том, чтобы кодировать k классов с помощью k -мерных наборов, приписывая i-й компоненте значение 1, если исследуемый образец принадлежит i-му классу, и 0 – в противоположном случае. Такой способ часто называют бабушкиным кодированием. Другой способ работы с многими классами – разбить задачу с k классами на k(k-1) подзадач, содержащих только по два класса. Окончательное присваивание элементу i-го номера класса осуществляется несложной булевой функцией, на вход которой подаются выходы подзадач. В этом случае число выходных элементов с ростом k растет как k ². Это так называемое 2-на-2 кодирование часто оказывается лучше, чем бабушкин метод. Рис. 2.2 иллюстрирует проблему кодирования выхода на примере двумерной задачи с тремя классами. С помощью 2-на-2 кодирования задача классификации решается, тогда как в бабушкином методе кодирования необходимо строить нелинейные разрешающие границы.

Объем сети

Правильный выбор размера сети имеет важное значение. Хорошую, и притом очень маленькую, модель построить просто невозможно, а слишком большая будет чересчур сильно приспосабливаться к обучающим данным и плохо аппроксимировать настоящую задачу. Обычно начинают с сети небольшого размера и постепенно увеличивают ее, пока не будет достигнута нужная точность. При этом обучение сетей на каждом шаге проводится независимо. При другом подходе применяется «алгоритм само наращивания», когда по мере возникновения необходимости в сеть добавляются новые элементы, после чего заново происходит обучение. Совершенно другая идея лежит в основе деструктивного подхода: вначале берется сеть завышенного объема и из нее удаляются связи и узлы, существенно не влияющие на решение. При этом предполагается, что известна верхняя граница для размера сети – чаще всего ее, действительно, можно считать известной. При этом полезно иметь в виду «правило», согласно которому число весов всегда должно быть меньше, чем число обучающих примеров, – иначе сеть будет «привыкать» к данным, т.е. попросту запоминать их, и утрачивать способность к обобщению. Если априорные знания о задаче малы или отсутствуют, объем требуемой сети неизвестен. Например, когда разрешающая граница имеет сферическую форму (один класс внутри другого), число скрытых элементов, необходимых для аппроксимации границы, будет многочленом от N (размерности пространства входов). Для каких-то других задач может потребоваться экспоненциальное число узлов в сети, и наоборот, может оказаться, что задача большой размерности решается с помощью простых границ, составленных из отрезков.

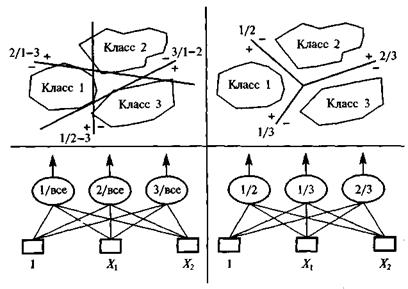
Рис. 2.2. Кодирование выхода на примере двумерной задачи с тремя классами. Слева — «бабушкин» метод кодирования и соответствующая сеть. Справа — 2-на-2 кодирование и соответствующая сеть

Однако правильный выбор объема сети – это еще не все. Надо определить значения всех весов, т.е. сеть должна «научиться» осуществлять нужное отображение. Для этого нужно выбрать эффективный алгоритм обучения. Самое простое здесь – взять классический алгоритм обратного распространения. Однако, часто более эффективными оказываются методы второго порядка. В последнее время было предложено большое количество новых алгоритмов, умень-шающих время обучения и отбрасывающих субоптимальные решения.

Выбор архитектуры сети

Обычно опробуется несколько конфигураций с различным числом элементов и структурой соединений. Одними из наиболее важных показателей являются объем обучающего множества и обеспечение способности к обобщению при дальнейшей работе, и нужного результата можно достичь на различных схемах. Чаще всего используются процедуры последовательного спуска (с подтверждающим множеством) или N-кратного перекрестного подтверждения. Могут быть применены и более мощные информационные критерии (IC): обобщенное перекрестное подтверждение (GCV), итоговая ошибка предсказания А какие (FРЕ), критерии Байеса (ВIС) и А какие (АIС). Для того чтобы улучшить способности к обобщению и устранить опасность переобучения, применяются также уменьшение весов и их исключение (прореживание дерева). При этом изменяется архитектура сети: удаляются некоторые связи и изучается, какое влияние они оказывали на эффективность.