Цель классификации

Рассмотрим, как нейронные сети с прямой связью (или многослойные персептроны — MLP, Multilaier Perceptron) используются в задачах классификации. В чем, собственно, заключается эта задача? Во-первых, в любой задаче классификации требуется отнести имеющиеся статические образцы (рукописные буквы, звуковые сигналы, характеристики финансового положения) к определенным классам. Эффективность классификации зависит от способа представления этих форм. В числе других здесь имеются следующие способы структурное представление и статистическое представление распознавания образов. В структурном распознавании образов образцы описываются тем, как они составлены из своих компонент, т.е. структурой, подобно тому, как это делается в грамматике языка. Распознавание в этом случае основывается на применении определенных синтаксических правил. При статистическом подходе к распознаванию образец представляется вектором х ÎÂ^N, компоненты которого представляют собой различные характеристики (дескрипторы) образца. Классификатор относит объект х^k к тому или иному классу С в соответствии с определенным разбиением N-мерного пространства, которое называется пространством входов.

При решении задачи распознавания статистическими методами важнейшее значение имеет правильный выбор способа статистического представления объекта. Тем самым, нужно проделать предварительную обработку данных. Для того чтобы выбрать характерные отличительные признаки объектов, требуется, как правило, серьезное изучение исходной проблемы. Например, в моделях банкротства банков важное значение имеют такие показатели, как опыт в управлении фондами и соответствие требованиям адекватности капитала. Различные наборы признаков приводят к разным распределениям. При этом в разных вариантах дисперсия и свойства выпуклости кластеров во входном пространстве могут сильно отличаться, соответственно, при их разделении потребуется проводить границы разной степени сложности – от линейных до сильно нелинейных. Чем лучше была сделана предварительная обработка, тем легче будет решена задача классификации.

Прежде всего нужно определиться с выбором уровня сложности. В реальных ситуациях часто бывает так, что имеется лишь относительно небольшое число образцов, а структура данных позволяет выделить следующие три уровня сложности (рис. 2.1). Первый (простейший) – когда классы можно разделить прямыми линиями (или гиперплоскостями, если пространство имеет размерность больше двух). Этот случай называется линейной отделимостью. Во втором случае одной гиперплоскости для разделения недостаточно (нелинейная отделимость), а в третьем случае классы пересекаются, и поэтому разделить их можно только в вероятностном смысле.

В идеальном варианте предварительная обработка должна дать такой набор признаков, чтобы задача оказалась линейно отделимой, – классификация после этого существенно упрощается. К сожалению, это редко удается сделать. Как правило, в нашем распоряжении имеется лишь ограниченный набор образцов, и часть из них используется для проведения границ, разделяющих классы («построение классификатора»). Качество классификатора по отношению к имеющимся примерам измеряется оценкой. При последующей работе классификатора с новыми образцами происходит обобщение.

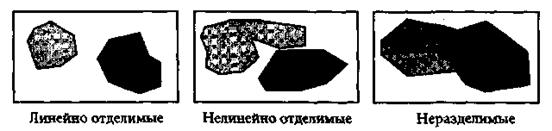
Рис. 2.1. Различные степени сложности в представлении классов. Заштрихованные фигуры изображают совокупность всех возможных образцов