Самоорганизующиеся сети

Введенную Кохоненом (см., например, [8]) «самоорганизующуюся карту признаков» можно рассматривать как вариант нейронной сети. Сеть такого типа рассчитана на самостоятельное обучение: во время обучения сообщать ей правильные ответы необязательно. В процессе обучения на вход сети подаются различные образцы. Сеть улавливает особенности их структуры и разделяет образцы на кластеры, а уже обученная сеть относит каждый вновь поступающий пример к одному из кластеров, руководствуясь некоторым критерием «близости».

Сеть состоит из одного входного и одного выходного слоя (рис. 1.15). Количество элементов в выходном слое непосредственно определяет, сколько различных кластеров сеть сможет распознать. Каждый из выходных элементов получает на вход весь входной вектор. Как и во всякой нейронной сети, каждой связи приписан некоторый синаптический вес. В большинстве случаев каждый выходной элемент соединен также со своими соседями. Эти внутрислойные связи играют важную роль в процессе обучения, так как корректировка весов происходит только в окрестности того элемента, который наилучшим образом откликается на очередной вход.

Выходные элементы соревнуются между собой за право вступить в действие и «получить урок». Выигрывает тот из них, чей вектор весов окажется ближе всех к входному вектору в смысле расстояния, определяемого, например, евклидовой метрикой. У элемента-победителя это расстояние будет меньше, чем у всех остальных. На текущем шаге обучения менять веса разрешается только элементу-победителю (и, может быть, его непосредственным соседям); веса остальных элементов при этом как бы заморожены. Выигравший элемент измененяет свой весовой вектор, немного перемещая его в сторону входного вектора. После обучения на достаточном количестве примеров совокупность весовых векторов с большой точностью приходит в соответствие со структурой входных примеров – векторы весов в буквальном смысле моделируют распределение входных образцов.

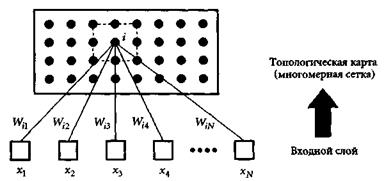
Рис. 1.15. Самоорганизующаяся сеть Кохонена. Изображены только связи, идущие в 1-й узел. Окрестность узла показана пунктиром

Очевидно, для правильного понимания сетью входного распределения нужно, чтобы каждый элемент сети становился победителем одинаковое число раз – весовые векторы должны быть равновероятными. Один из возможных способов осуществления этого механизма следующий: в расстояние между входным и весовым вектором вносится некоторая добавка, положительная для тех элементов, которые часто выигрывают, и отрицательная для тех, которые чаще проигрывают. Таким образом, шансы проигрывающих повышаются, и вся картина выравнивается. Величина добавки меняется в процессе обучения в соответствии с изменениями частоты выигрышей. Перед началом работы в сети Кохонена векторы весов должны быть случайно распределены по единичной сфере,а все весовые и входные векторы должны быть нормированы на единицу.