Вероятностная классификация

При статистическом распознавании образов оптимальный классификатор относит образец х^k к классу С, руководствуясь решающим правилом Байеса. Для двух классов оно выглядит так:

• Отнести х^k к C₁, если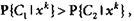

• Отнести х^k к С₂, если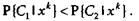

Здесь 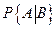- условие вероятность события А при условии, что произойдёт событие В.

Смысл правила простой: образец х^k относится к группе, имеющей наибольшую апостериорную вероятность. Это правило оптимально в том смысле, что оно минимизирует среднее число неправильных классификаций. Если имеется такая пара функций {j₁(x),j₂(x)}, что выполнены условия:

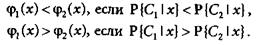(2.1)

то байесовское соотношение между априорной и апостериорной вероятностью сохраняет силу, и поэтому эти функции можно использовать в качестве упрощенных решающих функций. Так имеет смысл делать, если эти функции строятся и вычисляются более просто.

Хотя правило выглядит очень простым, применить его на практике оказывается трудно, так как бывают неизвестны апостериорные вероятности (или даже значения упрощенных решающих функций). Их значения можно оценить. В силу теоремы Байеса апостериорные вероятности можно выразить через априорные вероятности и функции плотности по формуле 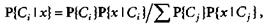где j – номер класса. Таким образом, правило Байеса для произвольного числа классов принимает вид:

• Отнести х к С_i, если 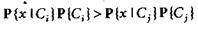для всех j ≠ i.