Методы с использованием неопределенных множителей Лагранжа.

Существует большое количество практических задач, в которых необходимо оптимальным образом распределить заданное количество ресурсов, т.е. решить задачу оптимизации, при наличии ограничений на независимые переменные, записанных в виде равенств.

Предположим, что целевая функция: R=R(x_i) -> ext2

i=1,n

Её независимые переменные x_i взаимосвязаны с собой в виде функциональной зависимости:

Φ_k(x_i)=0, k=1,m

Достаточно просто задача оптимизации решается, если ее размерность n равна количеству ограничений m. В этом случае задача сводится к поиску определенного набора дискретных значений x_i путем решения системы Φ_k(x_i)=0, при подстановке которого в значение целевой функции можем найти ее оптимальное значение. В иных случаях (n не равно m) применяется метод Лагранжа, его суть заключается в следующем:

Каждое из ограничений Φ_k(x_i)=0 домножается на неопределенные множители λ_k и формируется новая целевая функция Φ(х, λ), называемая функцией Лагранжа:

Φ(х, λ)=R(x)+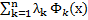

Решение задачи оптимизации в дальнейшем связано с нахождением таких x и λ, которые обращают в 0 частные производные функции Лагранжа по всем независимым переменным. Иными словами должна быть решена система уравнений:

Полученное решение системы обязательно должно быть проверено на достаточность.