Глобальные и локальные экстремумы целевой функции

При отыскании оптимума целевой функции задачей является нахождение такой совокупности значений независимых переменных, которые обеспечивают действительно наибольшее или наименьшее значение функции, иными словами в точке оптимума обязательно должно выполняться условие:

R(x_опт)<=R(x) х принадлежит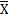

Которое справедливо для любогоx формирующего область определения функции. Такая точка называется глобальным экстремумом.

Кроме того целевая функция может иметь ряд точек x^(k), k= 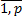для которых вышеупомянутое условие справедливо лишь в окрестности этих точек. Такие оптимумы носят название локальных экстремумов.

Поскольку для сложных нелинейных функций вид поверхности установить сложно, становится очевидными трудности отыскания глобальных экстремумов. Одним из способов нахождения глобального экстремума является старт из разных начальных точек.