Характеристика методов решения задач оптимизации

При решении конкретной оптимизационной задачи исследователь должен выбрать метод, который позволит получить решение с наивысшей эффективностью.

Под эффективностью решения задачи понимается точность получаемого решения и быстродействие. Выбор того или иного метода зависит от вида постановки задачи оптимизации и типа используемой математической модели(если таковая имеется).

Под видом постановки оптимизационной задачи понимается вид целевой функции и ограничения, если таковые имеются. В настоящее время все оптимизационные методы объединены в семь основных групп:

1. Методы исследования функций на базе классического анализа.

2. Методы с использованием неопределенных множителей Лагранжа.

3. Вариационное исчисление.

4. Принцип максимума.(Понтрягина)

5. Динамическое программирование.

6. Линейное программирование.

7. Методы нелинейного программирования.

Последние две группы часто объединяются в единую, под названием «Методы математического программирования».

Методы, формирующие первую группу, предназначены для решения несложных практических задач, в которых критерий оптимальности записан в несложном аналитическом виде. Это должно позволить получать также несложные аналитические выражения для производных целевой функции, анализируя которые, принимают решения о наличии экстремума. Ограничения отсутствуют.

Вторая группа предназначена для решения такого же класса задач, что и первая группа, но при наличии на независимые переменные, записанных в виде равенств.

Третья группа предназначена для решения задач оптимизации, в которых критерий оптимальности задан функционалом типа:

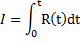
Где интегральная оценка R(t) – функция состояния объекта в любое время t.

Четвертая группа. Областью применения методов, формирующих эту группу, являются задачи, в которых и критерий оптимальности и математическая модель записаны в виде дифференциальных уравнений.

Пятая группа.Динамическое программирование является эффективным способом решения оптимизационных задач, в которых объект оптимизации представлен многостадийным производством, а критерий оптимальности записывается в виде аддитивной оценки критериев отдельных стадий. Закон управления процессом на каждой стадии рассматривается отдельно, для его нахождения могут с успехом использоваться методы первой и седьмой групп.

Шестая группа. Методы предназначены для решения задач оптимизации, в которых критерий оптимальности и ограничения, накладываемые на независимые переменные, записаны в линейном виде. Применяется для решения задач, в которых необходимо оптимальным образом распределить ограниченное количество ресурсов. Чаще всего используется для решения транспортных задач.

Для решения задач невысокой размерности с успехом может быть применен графический способ решения (см. лаб. №1). Для многоразмерной оптимизационной задачи используется аналитический симплекс-метод.

Седьмая группа.Эти методы применяются для решения большинства практических задач, особенно в тех случаях, когда критерий оптимальности задается в неявном виде. Областью применения данных методов являются также задачи, в которых критерий оптимальности записывается в нелинейном виде(как правило вид зависимости очень сложен), что не позволяет использовать аналитические методы. Иногда эти методы называют методами прямого поиска.