Методы исследования функций на базе классического анализа

Областью применения данных методов являются задачи, в которых критерий оптимальности или целевая функция представлен явным несложным аналитическим видом, что позволяет находить и анализировать также аналитические выражения для производных целевой функции. Ограничения на независимые переменные отсутствуют. Необходимым условием экстремума функции является равенство нулю первой производной или ее отсутствие. Равенство нулю или отсутствие первой производной является лишь необходимым условием наличия экстремума в точке. Поскольку функция может иметь такие точки ,в которых условие выполняется, а экстремума нет, поэтому получаемое при решении задачи условие обязательно должно быть проверено на достаточность. Существует три способа проверки.

1 Способ: исследование значений функции. При этом способе сравниваются значения функции, рассчитанные в точке подозрительной на экстремум и в двух точках, лежащих в ε-окрестности этой точки.

2 Способ: исследование знаков первой производной, суть способа заключается в сравнении знаков производной в окрестности точки подозрительной на экстремум. Если производные имеют разные знаки, экстремум в точке имеется.

3 Способ: сравнение знаков высших производных. Применение данного способа проверки на достаточность подразумевает, что целевая функция непрерывна сама и имеет также непрерывные первую и более высокого порядка производную.

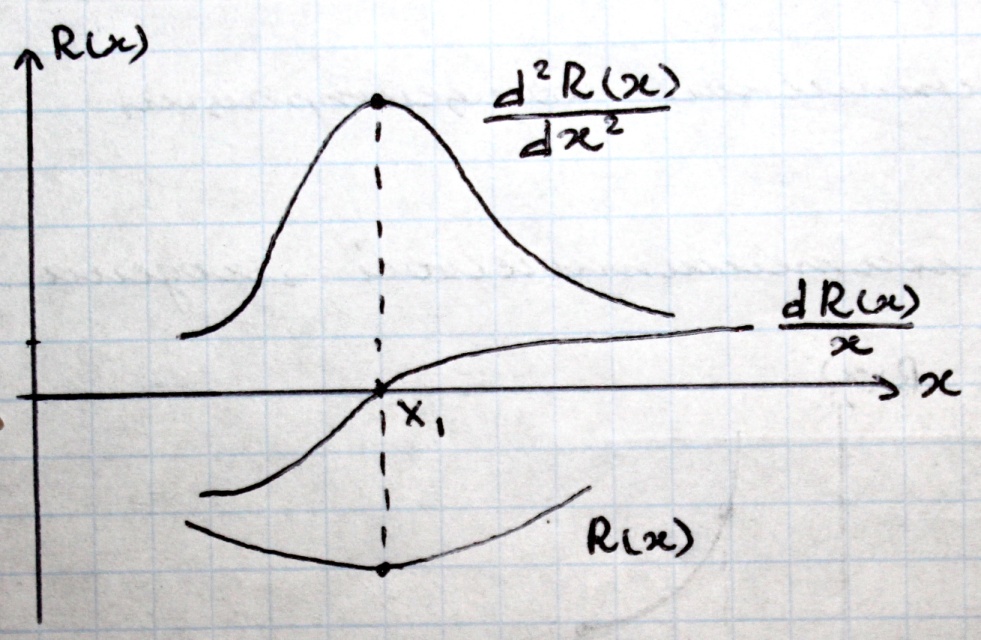
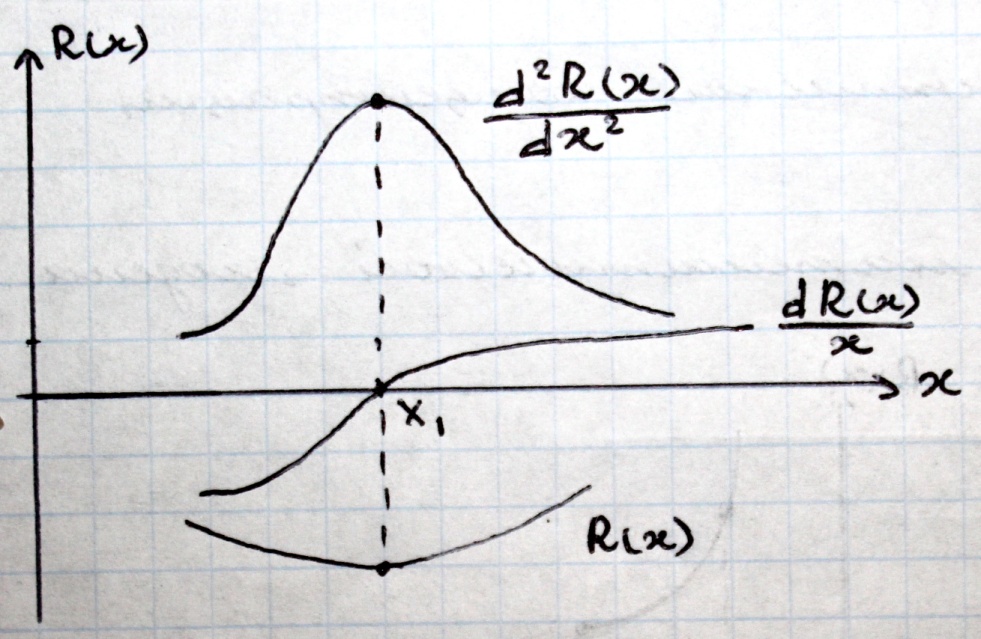
Достаточным условием наличия экстремума в точке является неравенство нулю второй производной. О типе экстремум судят по знаку второй производной: отрицательная в точке максимума, положительная в точке минимума. Для наличия экстремума необходимо, чтобы четная производная была отлична от нуля.