Свойство 3 точек для ДЛО.

Теорема. Для любых 3 различных точек 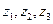и любых 3 различных точек 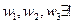ДЛО, переводящее точки: 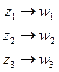по этой таблице из 3 значений ДЛО восстанавливается ! образом.

Доказательство: 1) 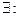В частном случае сначала 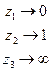. Предъявим в явном виде исходную функцию. 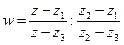построили. Ангармоническое (или двойное) отношение четырёх точек, а именно точек 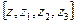. Заметим, что решив задачу в частном случае, мы решили её и в общем. Т.е. 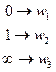, таким образом, 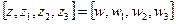в неявном виде мы доказали .

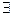2) !: Пусть 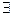два искомых ДЛО: 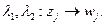Надо взять 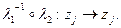т.е. имеем 3 неподвижные точки следовательно это отображение тождественно, т.е. 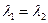, иначе напишем уравнение на неподвижные точки: 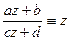- уравнение не выше 2 степени 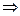корней не больше 2. (Вообще-то решений всегда ровно 2 – т.е. две неподвижные точки.)

Следствие: Ангармоничное отношение инвариантно относительно ДЛО.

Задача: 4 точки лежат на одной окружности (или прямой) 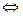их двойное отношение вещественно.