Групповое свойство.

Теорема. Все ДЛО образуют группу относительно композиции.

Доказательство: очевидно (проверить).

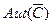- обозначим так группу для ДЛО.

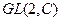- рассмотрим такую группу. И рассмотрим отображение: 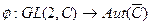, т.е. 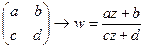, 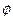- гомоморфизм (Проверить). Найдём ядро этого гомоморфизма.

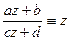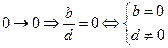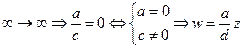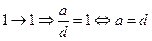, , , но , таким образом 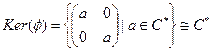(изоморфно). Тогда

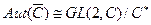или 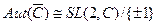- это матричная реализация.