Стереографическая проекция.
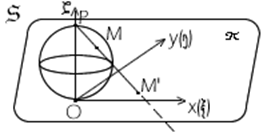
Имеем сферу S с диаметром 1. Она касается некоторой плоскости 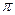 . Точка касания 0. Диаметрально противоположная точка – Р. Возьмём на сфере любую точку М. Через точки Р и М проведём прямую, которая
. Точка касания 0. Диаметрально противоположная точка – Р. Возьмём на сфере любую точку М. Через точки Р и М проведём прямую, которая 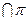 в точке М’. Это стереографическая проекция сферы на плоскость. Так отображение взаимно однозначное. Есть обратное отображение. Получим координатные формулы для стереографической проекции.
в точке М’. Это стереографическая проекция сферы на плоскость. Так отображение взаимно однозначное. Есть обратное отображение. Получим координатные формулы для стереографической проекции.
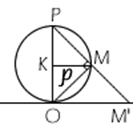
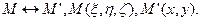
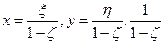 - коэффициент подобия. КМ – обозначим за
- коэффициент подобия. КМ – обозначим за 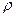 .
. 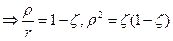 , (ОМР – прямой угол, среднее геометрическое, r = OM’).
, (ОМР – прямой угол, среднее геометрическое, r = OM’). 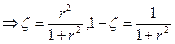 , следовательно окончательные формулы и формулы для обратного отображения:
, следовательно окончательные формулы и формулы для обратного отображения:
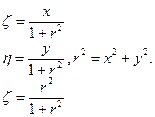
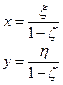
Теорема1 (Свойство конформности для стереографических проекции). Стереографическая проекция сохраняет углы между кривыми.
Доказательство: На сфере проведём 2 гладкие кривые. Рассмотрим на 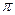 образы этих кривых и докажем что углы равны (Геометрическое доказательство). Через М проводим 2 касательные
образы этих кривых и докажем что углы равны (Геометрическое доказательство). Через М проводим 2 касательные 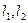 к кривым. Через точку Р и
к кривым. Через точку Р и 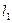 проведём плоскость. Она пересечёт
проведём плоскость. Она пересечёт 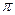 по
по 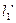 . Аналогично и для
. Аналогично и для 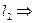 получим
получим 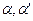 . Проведём
. Проведём 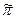 - касательную плоскость к сфере в точке Р.
- касательную плоскость к сфере в точке Р. 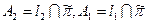 . Рассмотрим
. Рассмотрим 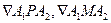
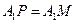 - две касательные.
- две касательные. 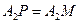 - аналогично.
- аналогично. 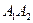 - общая сторона.
- общая сторона. 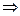 треугольники равны (по 3ему признаку J).
треугольники равны (по 3ему признаку J). 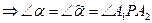 . Но
. Но 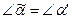 (углы с параллельными сторонами)
(углы с параллельными сторонами) 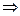 ч.т.д.
ч.т.д. 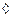
Теорема2 (Круговое свойство). Стереографическая проекция устанавливает взаимно однозначное соответствие между окружностями на сфере и окружностями на плоскости (прямую на плоскости называем здесь окружностью).
Доказательство: (Координатное). Окружность на сфере – линия пересечения с некоторой плоскостью, т.е. 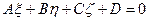 - общее уравнение окружности на сфере.
- общее уравнение окружности на сфере. 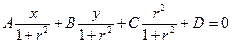 . Домножаем на
. Домножаем на 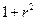 :
: 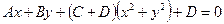 - общее уравнение окружности на плоскости, если
- общее уравнение окружности на плоскости, если 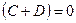 ,то прямая.
,то прямая. 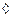
Дата добавления: 2015-09-02; просмотров: 4763;
