Свойство конформности для ДЛО.

Теорема. ДЛО сохраняет углы между кривыми.

Доказательство: Достаточно доказать теорему для простейших ДЛО. Для первых двух очевидно. Докажем для инверсии: Для симметрии относительно прямой – очевидно. Осталось рассмотреть для симметрии относительно окружности. Сделаем стереографическую проекцию, она сохраняет углы. Вспомним: 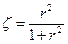, подставим 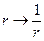. Получится: 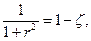таким образом, 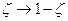- симметрия относительно экваториальной плоскости (на сфере). Но при симметрии углы сохраняются.

ДЛО сохраняют углы не только по величине, но и по направлению(т.к. композиция двух симметрий).