Свойство симметрии для ДЛО.
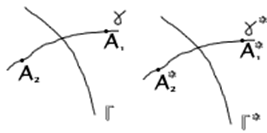
Теорема. Если ДЛО переводит окружность Г в окружность Г*, то точки, симметричные относительно Г, оно переводит в точки, симметричные относительно Г*.
Доказательство: Вспомним критерий симметричности: 2 точки А1,А2 – симметричны относительно окружности Г 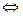 любая окружность
любая окружность 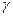 , проходящая через эти 2 точки пересекает Г под прямым углом.(доказательство этого самостоятельно). Доказательство очевидно после применения этого критерия. Через точки
, проходящая через эти 2 точки пересекает Г под прямым углом.(доказательство этого самостоятельно). Доказательство очевидно после применения этого критерия. Через точки 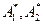 проведём
проведём 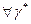 - окружность. Ее прообраз – окружность
- окружность. Ее прообраз – окружность 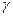 .По условию А1,А2 симметричны
.По условию А1,А2 симметричны 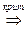 Г и
Г и 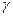 пересекаются под прямым углом
пересекаются под прямым углом 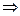 образы Г и
образы Г и 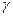 пересекаются под прямым углом
пересекаются под прямым углом 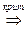 точки
точки 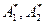 симметричны.
симметричны. 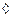
Дата добавления: 2015-09-02; просмотров: 1150;
