Толқындық функция және оның статистикалық мағынасы

Микробөлшектерді бейнелеу үшін ықтималдық амалды қолдану қажеттігі квантық теорияның маңызды өзгешелігі болып табылады. Сонда де-Бройль толқындарын ықтималдық толқындары ретінде мағыналауға, яғни микробөлшектердің кеңістіктің әртүрлі нүктелерінде табылу ықтималдығы толқындық заң бойынша өзгереді деп санауға бола ма? – деген сұрақ туады. Де-Бройль толқындарын осылай түсіндіруге болмайды, өйткені осы жағдайда кеңістіктің кейбір нүктелерінде бөлектің табылу ықтималдығы теріс болуы мүмкін, бұл мағынасыздық.

Осы қиындықты жою үшін 1926 ж. неміс физигі М. Борн толқындық заң бойынша ықтималдықтың өзі емес, ықтималдық амплитудасы деп аталатын шама өзгереді деп ұйғарды. Осы шама 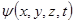функциясы арқылы белгіленеді, ол толқындық функция деп аталады.

Сонымен, кеңістіктің қайсыбір нүктесінде берілген уақыт мезетінде бөлшектің табылу ықтималдығының үлестірілуін бейнелеу үшін толқындық функция (немесе пси-функция) деп аталатын 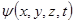функциясы енгізіледі. Ал ықтималдық былай анықталады:

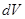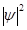Бөлшектің көлем элементіне болу ықтималдығы және 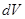көлем элементіне пропорционал:

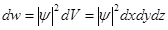. (3)

Физикалық мағынаға 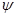функциясының өзі емес, оның модулінің квадраты 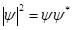ие, мұндағы 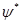– комплекс 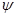-мен түйіндес функция. 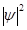шамасы ықтималдық тығыздығы мағынасын береді:

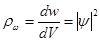, (4)

яғни кеңістіктің берілген нүктесінде бөлшектің табылу ықтималдығын анықтайды. Басқа сөзбен айтқанда, 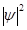шамасымен де Бройль толқындарының интенсивтігі анықталады.

Бөлшектің орнын барлық кеңістік бойынша қарастыру керек. Бөлшектің әйтеуір бір жерде болатындығы ақиқат, демек, бөлшекті бүкіл көлемнің әйтеуір бір жерінде табылу ықтималдығы ақиқат нәрсе. Осындай жағдайдың ықтималдығы бірге тең. Сондықтан

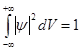немесе 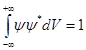. (5)

Осы теңдік нормалау шарты деп аталады, ал осы шартты қанағаттандыратын 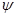функциясы нормаланған болады.

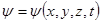, сондықтан нормалау шарты кез келген уақыт мезеті үшін орындалуы тиіс.

Толқындық функция микробөлшектер күйінің негізгі сипаттамасы болып табылады.