Шредингердің уақыттық және стационар теңдеуі

Классикалық механикада күш және өріс әсерінен қозғалатын бөлшектің координаттары мен импульстарының бұрынғы және болашақ мәндерін қозғалыс теңдеуі арқылы бірмәнді анықтауға болады (егер бұлардың қайсыбір уақыт мезетінде мәндері берілген болса). Ал микробөлшектер үшін бұл әдіс қолдануға келмейді.

Себеп мынада. Микробөлшектердің корпускулалық әрі толқындық қасиеттері болатындығына әбден көз жеткізілді. Осыдан әр түрлі күш өрістерінде бөлшектің қозғалысын қарастырғанда бұлардың толқындық табиғатын ескеру қажет екендігі келіп шығады. Сонды бөлшек қозғалысын бейнелеу үшін 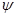толқындық функция пайдаланылады. Ендігі негізгі мәселе 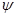толқындық функцияның кеңістіктегі және уақыт бойынша өзгерісін бейнелейтін жалпы заңды немесе толқындық өрістің қозғалыс заңын тағайындау болып табылады.

Зат бөлшектерінің толқындық қасиеттері жайындағы де-Бройль идеясын дамыта келе, австрия физигі Э. Шредингер өзінің атақты теңдеуін ұсынды (1926). Осы теңдеу әр түрлі күш өрістерінде қозғалатын бөлшектің толқындық функцияларын табуға мүмкіндік береді. Шредингер теңдеуі былай жазылады:

, (1)

мұндағы т – бөлшек массасы, і – жорамал бірлік, U – бөлшектің потенциалдық энергиясы, – Лаплас операторы.

Шредингер теңдеуі – бұл Ньютон механикасының теңдеулері, электромагниттік өріс үшін Максвелл теңдеулерімен және т.б. қатар қазіргі заманғы физиканың іргелі теңдеулерінің бірі, және де ол қорытылып шығарылмайды. Оны бастапқы негізгі ұйғарым деп қарастыру керек. Шредингер теңдеуінің дұрыстығы теория нәтижелерінің эксперимент деректерімен толық үйлесуімен, және де практикада қолданыс тапқан, мысалы, мазерлерде, лазерлерде, жартылай өткізгішті қондырғыларды және т.т. көптеген болжаулармен расталады.

Кванттық теорияда ерекше ролді стационарлық күйлер атқарады, бұларда барлық бақыланатын физикалық шамалар уақыт өткенде өзгермейді.

Стационарлық күйлер үшін Шредингер теңдеуі:

. (2)

Оны мына түрде жазуға болады:

. (3)

Шредингер теңдеуі берілген күйдің толқындық функциясын табуға, демек кеңістіктің әр түрлі нүктелерінде бөлшектің болу ықтималдығын анықтауға мүмкіндік береді.