Доказательство. Пусть R и Q - символы, которые не встречаются среди символов алфавитов систем P1 и P2.

Пусть R и Q - символы, которые не встречаются среди символов алфавитов систем P₁ и P₂.

1. Определим систему P_U. Основной алфавит и алфавит переменных этой системы получаются объединениями основных алфавитов и алфавитов переменных систем P₁ и P₂.

Вспомогательный алфавит системы P_U состоит из символов вспомогательных алфавитов для P₁ и P₂, а также символов R и Q.

Множество продукций системы P_U состоит из продукций, получаемых из продукций P₁ приписыванием всем образцам слева символа R, а также продукций, получаемых из продукций системы P₂ с помощью аналогичного приписывания символа Q.

Кроме того, в P_U добавлены продукции:

и .

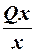Покажем, что в системе P_U выводятся те и только те слова, которые принадлежат W₁ 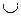W_2.

Это следует из того, что некоторое слово x выводится в системе P_U тогда и только тогда, когда в этой системе выводится либо слово Rx, либо слово Qx.

Последнее равносильно тому, что x выводится либо в P₁, либо в P₂. Поэтому в P_Uвыводится множество слов W₁ 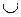W₂.

2. Определим систему Поста P_I.

Алфавиты этой системы определяются так же, как это было определено для системы P_U.

Продукции системы P_I получаются из продукций P₁ и P₂ приписыванием ко всем образцам в них слева символов R и Q соответственно.

К этим продукциям добавляется еще одна

.

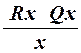Видно, что в системе P_I выводятся такие и только такие слова x, которые могут быть выведены как в P_1, так и в P₂.

Поэтому множество слов, выводимых в системе P_I, равно
W₁ 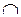W₂.