ОПРЕДЕЛЕНИЕ. Числовая функция f:Nk ® N вычисляется системой P, если " m1,
Числовая функция f:Nk ® N вычисляется системой P, если " m1, ... , mkÎ N(f(m1, ... , mk) = mk+1 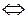 в системе P выводится слово “f(
в системе P выводится слово “f( 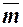 1, ... ,
1, ... , 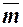 k) =
k) = 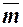 k+1“).
k+1“).
В качестве примера рассмотрим систему Поста, в которой вычисляется функция следования S(x) = x + 1.
Такая система имеет вид: P = (A, B, V, P), где
A = {0, 1, S, (, ), =}, B = {N}, V = {x, y}, а P - это следующие продукции.
1. Вспомогательные продукции, позволяющие выводить только правильные записи чисел из N в двоичной системе:
p1: N 0, p2: N1, p3: N10, p4: N 11,
p5:  , p6:
, p6: 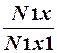 .
.
2. Продукция, задающая правило прибавления единицы к четным числам:
p7: 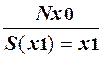 ;
;
3. Продукция, задающая правило прибавления единицы к нечётным числам (запись которых заканчивается единицей):
p8: 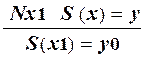 .
.
В частности, следующая последовательность образует вывод слова S(101) = 110:
1. N1 аксиома p2;
2. N10 из N1 с помощью p5;
3. N101 из N10 с помощью p6;
4. S(10) = 11 из N10с помощью p7;
5. S(101) = 110из N10и S(10) = 11 с помощью p8.
В приведенной системе вычисляется достаточно простая арифметическая функция. Однако добавление к ней небольших количеств новых продукций, использующих другие функциональные символы, позволяет получать системы Поста, вычисляющие новые, в том числе более сложные, числовые функции.
Например, для вычисления функции p(x, y) = x + y достаточно добавить к уже имеющимся продукциям следующие новые продукции:
p9: 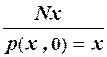 ; p10:
; p10: 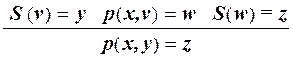 .
.
В продукции p9 представлено правило прибавления к произвольному числу минимального неотрицательного целого числа.
В 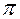 10 записано рекурсивное правило сложения двух произвольных чисел, использующего значение суммы первого числа и числа на единицу меньше, чем второе слагаемое.
10 записано рекурсивное правило сложения двух произвольных чисел, использующего значение суммы первого числа и числа на единицу меньше, чем второе слагаемое.
Продукции p9 и p10 соответствуют рекурсивному определению функции p(x, y). Из них продукция p9 задаёт граничное условие, а p10 представляет рекурсивное правило, в котором значение p(x, y) выражается через значение p(x, v), где v = y - 1.
Используя продукции, позволяющие вычислять функции S и p, можно определять системы Поста, в которых вычисляются и другие функции.
Например, функция усеченной разности: d(x, y) = x -y вычисляется с помощью двух продукций, добавляемых к продукциям p1 - p10:
p11 : 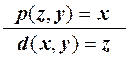 , p12 :
, p12 : 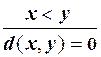 .
.
Множество всех числовых функций, вычисляемых системами Поста, совпадает с классом частично-рекурсивных функций.
Справедливость приведенного утверждения следует из теоремы 9.4.
Дата добавления: 2015-09-18; просмотров: 514;
