Ускорение

Ускорением называют векторную величину, характеризующую быстроту изменения вектора скорости, и количественно определяемую соотношением

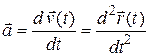(1.22)

Поскольку скорость 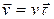(1.6) , то, по аналогии двумя составляющими вектора скорости, характеризующими изменение радиус-вектора частицы, логично выделить две составляющих ускорения:

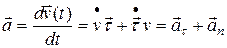. (1.23)

Направление составляющей 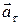совпадает с 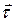, т.е с касательной к траектории движения и скоростью, поэтому ее называют тангенциальным ускорением.Эта составляющая ускорения определяет быстроту изменения вектора скорости по модулю.

Составляющая 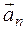направлена перпендикулярно скорости ( 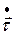– производная орта) и называется нормальным ускорением. 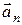характеризует быстроту изменения скорости по направлению.

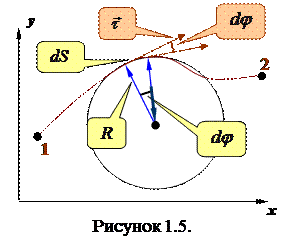
Обсудим более подробно чем определяется нормальное ускорение. Легко понять, что быстрота изменения направления вектора скорости, а значит и нормального ускорения, будет тем больше, чем сильнее искривлена траектория и чем больше модуль скорости перемещения частицы по траектории. Для количественной характеристики степени скривленности траектории используется величина, называемая кривизной траектории:если при перемещении вдоль траектории на расстояние 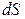(см.рис.1.5) касательная к траектории (а значит и вектор скорости) поворачивается на угол 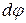, то кривизной траектории в данной ее точке называется:

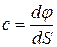. (1.24)

Величина R, обратная кривизне,

Гласно формуле (1.3)

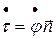(1.26)

.

где 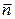- орт нормали к траектории, направленный в сторону поворота касательной к траектории .

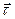Путь который проходит частица за время 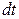с одной строны из геометрических соображений можно найти как

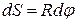. (1.27)

С другой стороны – 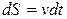. (1.28)

Приравнивая правые части этих соотношений, находим:

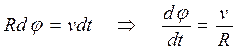. (1.29)

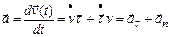
Тогда в соответствии с (1.23) Для

для нормального ускорения получаем:

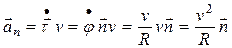. (1.30)