ВЫЧИСЛЕНИЕ ПРОЙДЕННОГО ПУТИ
Найдем общую формулу для вычисления пройденного частицей пути S в промежутке времени от 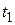 до
до 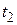 , если известна зависимость модуля вектора скорости от времени
, если известна зависимость модуля вектора скорости от времени 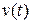 .
.
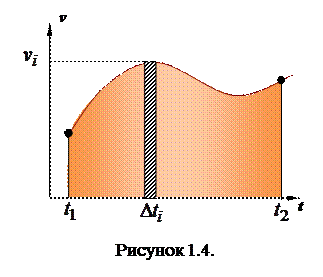 Допустим, что зависимость
Допустим, что зависимость 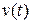 представлена графиком, показанным на рисунке 1.4. Разобьем мысленно проме-жуток времени
представлена графиком, показанным на рисунке 1.4. Разобьем мысленно проме-жуток времени 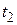 –
– 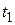 на N столь небольших отрезков
на N столь небольших отрезков 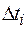 , чтобы можно было считать скорость
, чтобы можно было считать скорость 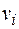 на отрезке
на отрезке 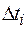 неизменной. Тогда путь
неизменной. Тогда путь 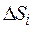 за каждый интервал
за каждый интервал 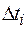 находится по формуле
находится по формуле 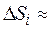
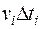 , а весь путь:
, а весь путь:
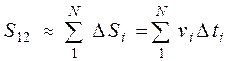 .м м (1.15)
.м м (1.15)
C геометрической точки зрения каждое из слагаемых в соотношении (1.15) представляет собой площадь прямоугольника высотой 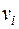 и основанием
и основанием 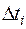 . Сумма (1.15) дает приблизительную площадь фигуры, ограниченной осью времени, графиком
. Сумма (1.15) дает приблизительную площадь фигуры, ограниченной осью времени, графиком 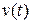 и прямыми t =
и прямыми t = 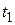 и t =
и t = 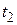 . Точное значение пути получится, если положить, что
. Точное значение пути получится, если положить, что 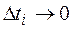 , а
, а 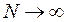 :
:
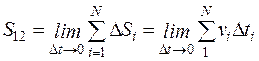 . (1.16)
. (1.16)
Выражение (1.16) представляет собой определенный интеграл от 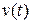 в пределах от
в пределах от 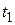 до
до 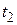 :
:
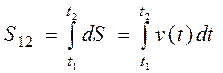 (1.17)
(1.17)
При этом геометрически пройденный путь изображается площадью, ограниченной графифком 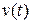 , осью времени и вертикальными отрезками, изображающими значения скорости в начальный и конечный момент.
, осью времени и вертикальными отрезками, изображающими значения скорости в начальный и конечный момент.
Если в соотношение (1.17) вместо 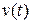 подставить вектор
подставить вектор 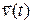 , то, поскольку в соответствии с определением
, то, поскольку в соответствии с определением 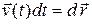 есть перемещение за
есть перемещение за 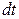 , интеграл
, интеграл
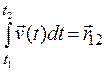 (1.18)
(1.18)
даст перемещение частицы за 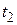 –
– 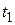 .
.
Дата добавления: 2015-09-14; просмотров: 720;
