КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

Рисунок 1.6.

Ограничимся рассмотрением вращения тел относительно неподвижной оси вращения ОО. Графически поворот тела на некоторый угол

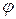можно задать в виде отрезка, с длиной, пропорциональной

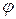и направленного по оси вращения так, что направление вращения тела и направление отрезка связаны между собою правилом правого винта. Можно доказать, что повороты на бесконечно малые углы (даже в общем случае, при сложных вращениях) складываются по правилу параллограмма, а значит являются векторами. В кинематике вращательного движения такие повороты играют роль перемещений в поступательном движении.

По определению угловой скоростью тела называется векторная величина

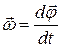. (1.32)

Вращение с постоянной называется равномерным. Его характеризуют периодом вращения

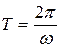(1.33)

И числом оборотов в единцу времени

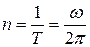(1.34)

Быстроту изменения угловой скорости по величине (а при произвольном вращении и направлению) характеризуют угловым ускорением:

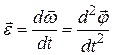. (1.35)

Отдельные точки вращающегося тела движутся с различными скоростями. Точка, находящаяся на расстоянии 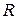от оси вращения за время 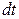проходит путь

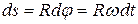. (1.36)

Следовательно, ее линейная скорость

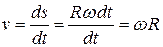. (1.37)

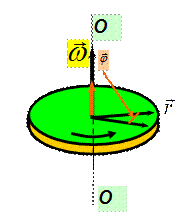
Соотношение (1.37) связывает модули векторных величин, входящих в него. Для того, чтобы учесть векторный характер величин и математически связать и указать их направления зададим положение вращающейся точки посредством радиус-вектора 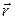, проведенного из точки, принадлежащей оси вращения (рисунок 1.7). Обозначим 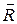вектор, проведенный перпендикулярно оси вращения к рассматриваемой точке. Модуль этого вектора R = 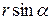. Векторное произведение 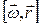направлено перпендикулярно плоскости, образованной векторам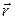и и 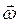, и совпадает по направлению с линейной скоростью точки. Модуль 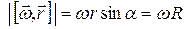. Следовательно, справедливо векторное соотношение:

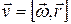(1.38)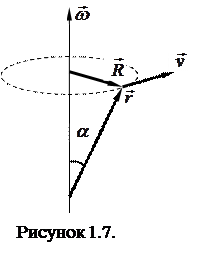

Наконец отметим, что нормальное ускорение может быть представлено с помощью формулы (1.37) в следующем виде:

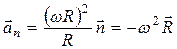, (1.39)

Поскольку вектор 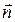направлен противоположно 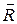, к центру окружности.

Тангенциальное ускорение 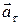также связано с угловыми характеристиками движения тела: если ось вращения не поворавчивается в пространстве и тело движется с угловым ускорением 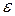, то тангенциальное ускорение

(1.40)

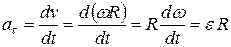<4 5 678 9 10 >

Дата добавления: 2015-09-14; просмотров: 700;