СКОРОСТЬ МАТЕРИАЛЬНОЙ ТОЧКИ
Предварительно сформулируем необходимые определения(см. рисунок 1.2):
Ø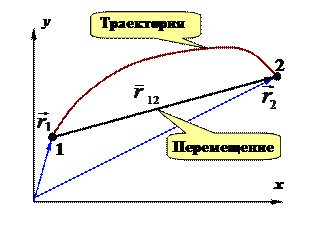 
Траекторией материальной точки будем называть воображаемую линию, вдоль которой движется частица. (Очевидно, что траектория – это, как и сама материальная точка, воображаемый объект, модель.)
Ø Путь,пройденный материальной точкой– скалярная величина, равная расстоянию, отсчитанному вдоль траектории при движении частицы из некоторой точки 1 в точку 2,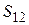 
.
Ø
|
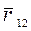, проведенный из точки 1 в 2 траектории. Очевидно, что перемещение 
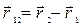. С другой стороны разность конечного и начального значения радиус-вектора есть его приращение: 
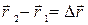. Поэтому можно считать, что можно считать, что перемещениепредставляет собойприращение радиус-вектора.
Движение частицы называется равномерным, если в любые равные промежутки времени частца проходит одинаковые пути (независимо от формы траектории!).
Важнейшим понятием кинематики является скорость материальной точки. На качественном уровне под скоростью в физике понимают векторнуювеличину, характеризующую быстроту перемеще-ния частицы по траектории и направление, в котором движется частица.
На бытовом уровне скорость можно найти, разделив путь, пройденный телом 
за промежуток времени 
, на величину этого промежутка. Такой расчет дает, очевидно, приближенное значение скорости, а о направлении скорости вообще ничего не позволяет сказать.
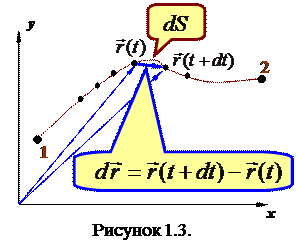Чтобы дать более строгое определение скорости поступим следующим образом: разобьем мысленно траекторию на участки 
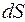, которые частица проходит за бесконечно малые промежутки времени 
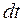(рисунок 1.3.). Каждому участку 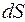соответствует перемещение 
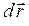за соответствующий 
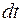. Для бесконечно малого 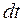можно утверждать, что модуль перемещения равен пути точки:
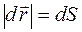, (1.4)
и траекторию можно считать состоящей из элементов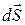 
, направленных в сторону перемещения частицы и совпадающих с 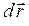. Можно считать, что за бесконечно малый 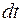движение тела не меняется. Отношение 
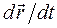дает векторную характеристику быстроты движения точки, модуль которой совпадает с традиционным представлением о скорости.
Поэтому по определению скоростью частицы называется производная ее радиус-вектора по времени:
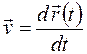(1.5)
Поскольку модуль приращения радиус-вектора за время 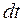совпадает по формуле (1.4) с элементом траектории 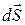, то в каждой точке траектории вектор скорости направлен по касательной к траектории в сторону движения частицы. Соответственно орт вектора скорости 
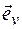совпадает с ортом касательной к траектории в данной точке, направленным в сторону движения частицы. Орт касательной к траектории принято обозначать 
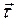. Поэтому для вектора скорости в данной точке траектории справедливо соотношение:
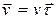(т.е.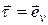 
) (1.6)
Учитывая, что выражение для радиус-вектора через его проекции на оси координат имеет вид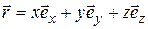 
, для вектора скорости можно записать представление через его проекции на оси координат 
:
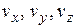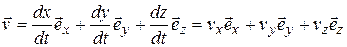, (1.7)
Как следует из соотношения (1.7), проекции вектора скорости на оси координат равны производным по времени проекций радиус-вектора, а составляющие вектора скорости по осям координат получаются умножением соответствующих производных на орты осей системы координат:
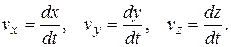(1.8)
(Напомним: проекции – это алгебраические скалярные величины, составляющие – это векторы, которые в сумме дают данный вектор).
В соответствии со своим определением вектор скорости характеризует быстроту изменения радус-вектора частицы. Радус-вектор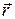 
может изменяться по модулю и по направлению. Следует предположить, что вектор скорости всегда можно представить в виде суммы двух векторов, один из которых характеризует изменение 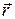только по модулю, а второй только по направлению. Действительно, как и любой вектор, 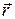можно представить в виде:
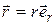. (1.9)
Находя производную по времени от этого выражения, получаем:
= 
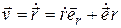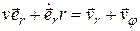, (1.10)
Составляющая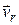 
направлена вдоль радиус вектора, а значит характерзует быстроту его изменения по мудулю. Направление второй составляющей, 
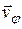, определяется производной орта радиус-вектора: 
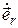. Как мы уже установили, производная орта определяется выражением (1.3)
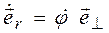. (1.11)
где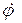 
– угловая скорость поворота радиус-вектора, а 
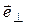- перпендикулярный к нему орт, направленный в сторону поворота. Следовательно, составляющая 
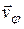перпендикулярна радиус-вектору и характеризует быстроту его изменения по направлению. Модуль скорости связан с составляющими вектора скорости соотношенем:
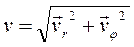. (1.12)
При движении точки изменяется ее радус-вектор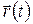 
и путь, пройденный ею путь 
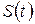от некоторой исходной точки. Если производная по времени от радиус-вектора дает по определению скорость частицы, то какой смысл имеет производная пути по времени?! Чтобы ответить на этот вопрос необходимо вспомнить о том, что модуль приращения радиус-вектора совпадает с элементом траектории 
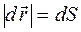. Тогда модуль соотношения, определяющего скорость,
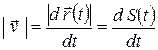. (1.13)
Таким образом, производная пути по времени дает модуль вектора скорости:
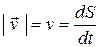, (1.14)
Дата добавления: 2015-09-14; просмотров: 733;