При криволинейном движении ускорение точки
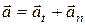 ,
, 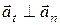 ,
,
Где – тангенциальное ускорение точки; – нормальное ускорение.
Модуль ускорения .
Проекции мгновенного ускорения на оси х, y, z
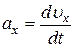 ,
, 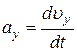 ,
, 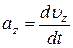 ;
;
модуль ускорения 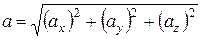 .
.
Кинематическое уравнение вращательного движения твердого тела (материальной точки по окружности радиусом 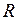 )
)
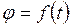 ,
,
где j – угол поворота тела; 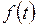 – некоторая функция времени.
– некоторая функция времени.
Угловая скорость тела (радиуса точки) 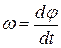 .
.
Угловое ускорение тела (радиуса точки) 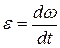 .
.
Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:
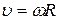 ,
, 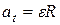 ,
, 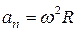 ,
,
где 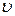 – модуль линейной скорости;
– модуль линейной скорости; 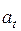 и
и 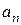 – модули тангенциального и нормального ускорений;
– модули тангенциального и нормального ускорений; 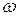 – модуль угловой скорости; e – модуль углового ускорения;
– модуль угловой скорости; e – модуль углового ускорения; 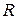 – радиус окружности.
– радиус окружности.
Модуль полного ускорения
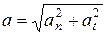 , или
, или 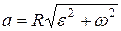 .
.
Угол a между полным 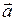 и нормальным
и нормальным 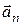 ускорениями
ускорениями
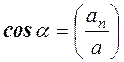 ,
, 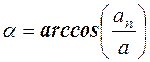 .
.
Кинематическое уравнение гармонических колебаний материальной точки вдоль оси Ох
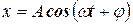 ,
,
где x – смещение; А – амплитуда колебаний; w – угловая, или циклическая частота; j – начальная фаза.
Скорость и ускорение материальной точки, совершающей гармонические колебания:
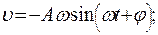
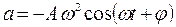 .
.
Сложение двух гармонических колебаний одного направления и одинаковой частоты 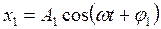 и
и 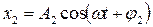 ; результирующее колебание
; результирующее колебание 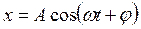 :
:
а) амплитуда результирующего колебания
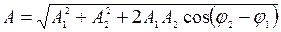 ;
;
б) начальная фаза результирующего колебания
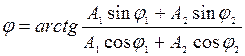 .
.
Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях 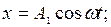
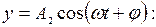
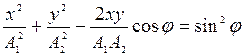 ;
;
а) 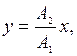 если разность фаз
если разность фаз 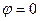 или
или 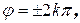 k=0,1,2,3,…;
k=0,1,2,3,…;
б) 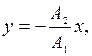 если разность фаз
если разность фаз 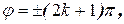 k=0,1,2,…;
k=0,1,2,…;
в) 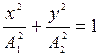 , если разность фаз
, если разность фаз 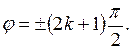
Импульс материальной точки массой т, движущейся со скоростью 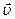 ,
, 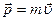 .
.
Дата добавления: 2015-11-04; просмотров: 677;
