Задание. Дана выборка , , i=1, N, N=100, где , — значения двух признаков исследуемых объектов.

Дана выборка 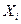, , 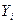i=1,…N, N=100, где 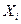, 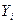— значения двух признаков исследуемых объектов.

Задача состоит в изучении характера зависимости между признаками X и Y.

Требуется:

1. Построить диаграмму рассеивания. Найти все выборочные числовые параметры: 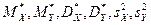, моду и медиану выборки для признаков X и Y. Построить гистограммы для признаков X и Y. Построить корреляционную таблицу.

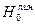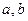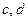2. Проверить гипотезу , что зависимость между признаками X и Y близка к линейной. Методом наименьших квадратов определить числа и , такие, чтобы уравнения линейных регресси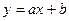й и 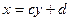наименее отклонялись от экспериментальных данных. Найти выборочный коэффициент корреляции 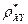. Изобразить обе линии регрессии на диаграмме рассеивания. Для проверки гипотезы 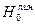используйте статистик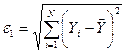и и .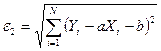

3. Проверить гипотезу 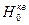, что зависимость между признаками X и Y близка к квадратичной. Методом наименьших квадратов определить числа 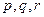такие, чтобы линия квадратичной регрессии 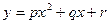наименее отклонялась от экспериментальных данных. Построить график линейной и параболической регрессий на диаграмме рассеивания. Для проверки гипотезы 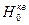используйте статистик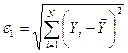и и .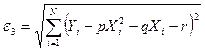

4. Сравнить между собой результаты пунктов 2 и 3 и ответить на вопрос задания о наличии и виде зависимости между признаками X и Y.

5. Построить доверительный интервал для математического ожидания признака Х.